ABSTRACT

High-quality, normal-incidence seismic reflection data confirm that tectonic deformation in the central Indian Ocean occurs at two spatial scales: whole lithosphere folding with wavelengths varying between 100 and 300 km, and compressional reactivation of crustal faults with a characteristic spacing of c. 5 km. Faults penetrate through the crust and probably into the upper mantle. Both types of deformation are driven by regional large intraplate stresses originating from the Indo-Eurasian collision. Numerical modelling of the spatial and temporal relationships between these two modes of deformations shows that, in agreement with geophysical observations, crustal faults are reactivated first with stick-slip behaviour. Subsequent lithospheric folding does not start until horizontal loading has significantly reduced the mechanical strength of the lithosphere, as predicted by elasto-plastic buckling theory. Modelling suggests that lithospheric folding does not develop in the absence of fault reactivation. Crustal fault reactivation, therefore, appears to be a key facilitating mechanism for oceanic lithospheric buckling in the central Indian Ocean.

INTRODUCTION

Recent single-channel and multi-channel seismic reflection studies (e.g. Bull and Scrutton, 1990, 1992; Pilipenko and Sivukha, 1991; Chamot-Rooke et al., 1993) have demonstrated the occurrence of two spatial scales of active tectonic deformation in the central Indian Ocean (Fig. 1), confirming earlier findings from single-channel seismic reflection data and compilations of earthquake, heatflow, geoid and gravity data (Weissel et al., 1980; Geller et al., 1983). The tectonic deformation is characterised by long wavelength undulations of oceanic basement and overlying sediments, and superimposed small scale faulting and folding (Fig. 2). The active intraplate deformation in the Indian Ocean is thought to be driven by large regional compressional stresses (e.g. Curray and Moore, 1971; Patriat and Achache, 1984). The large stresses may originate from the intense plate boundary processes (Indo-Eurasion collision; Indonesian subduction) surrounding this intraplate section of the Indo-Australian plate (Cloetingh and Wortel, 1985, 1986), or be related with a possible (nascent) diffuse plate boundary separating the Australian plate from the Indo-Arabian plate (Petroy and Wiens, 1989; DeMets et al., 1990; Gordon et al., 1990; Royer and Chang, 1991).

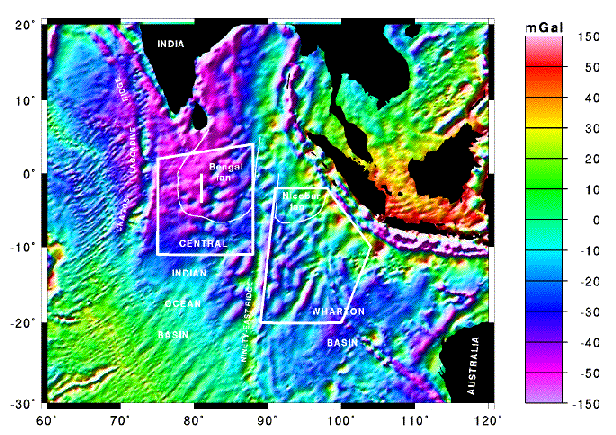
Figure 1. Illuminated relief image of ERS/GEOSAT/SEASAT derived free-air gravity anomalies (Sandwell and Smith, 1992) within the central Indian Ocean, and location map of main features. Boxes denote areas with consistently oriented linear trends in the gravity anomalies coinciding with axes of undulations of oceanic basement. Short line in left box denotes position of long seismic reflection line shown in Fig. 2.

Several tectonic models have been proposed to explain the undulations of the oceanic basement, from the interpretations of geoid and gravity anomalies, seismic reflection and refraction studies, and numerical and analogue modelling. Most support is given to flexural folding/buckling of the mechanically strong upper part of the lithosphere (Weissel et al., 1980; McAdoo and Sandwell, 1985; Karner and Weissel, 1990; Bull et al., 1992; Martinod and Davy, 1992; Molnar et al., 1993). Other proposed models are inverse boudinage of the oceanic crust caused by hydrodynamic viscous flow (Zuber, 1987; Leger and Louden, 1990), whole-crustal block faulting (Neprochnov et al., 1988), and a flexurally folded oceanic crust decoupled from the subcrustal lithosphere (Verzhbitsky and Lobkovsky, 1993). Theoretical studies (e.g. Timoshenko and Woinowsky-Krieger, 1959; Martinod and Davy, 1992) show that some kind of perturbation is required to destabilize the homogeneous shortening of a plate under compression in order to initiate other modes of deformation. In the previously mentioned modelling studies of intraplate deformation, various perturbation mechanisms have been assumed, such as line loading by the aseismic Ninety-East Ridge (McAdoo and Sandwell, 1985), the growth of mantle instabilities (Zuber, 1987), point loading by seamounts (Karner and Weissel, 1990), or surface sediment loading (Molnar et al., 1993).
However, regardless of the tectonic model and perturbation mechanism, all studies concentrate on reproducing only the long wavelength undulations of oceanic basement, neglecting the crustal faulting. This paper presents results of a numerical analysis using a nonlinear, elasto-plastic finite element method to analyse the temporal and spatial relationship between the two modes of tectonic deformation (lithospheric buckling and crustal fault reactivation) observed in the central Indian Ocean. The main objective is to investigate the role of crustal fault reactivation as a potential perturbation mechanism.

INTRAPLATE DEFORMATION IN THE CENTRAL INDIAN OCEAN

In the central Indian Ocean Basin, undulations of oceanic basement and, if present, sedimentary cover (Figs 2 and 3) trend E-W to NE-SW, with an amplitude of 1-2 km and a wavelength that increases from less than 100 km in the south to more than 300 km towards the north, averaging around 200 km (Weissel et al., 1980; Zuber, 1987; Neprochnov et al., 1988; Bull and Scrutton, 1992). The increase in wavelength is possibly related to the northward increase in age from 40 to 70 Ma of the oceanic lithosphere, and the associated increase in flexural rigidity (McAdoo and Sandwell, 1985). Within the Wharton Basin the undulations have similar wavelengths and amplitudes, but strike more consistently NE-SW (Stein et al., 1989; Pilipenko and Sivukha, 1991). In both basins, the axes of undulations are roughly perpendicular to directions of maximal horizontal compressional stress, as inferred from earthquake focal mechanism studies (Bergman and Solomon, 1985; Levchenko, 1989; Petroy and Wiens, 1989) and numerical computations of the Indo-Australian plate stress field (Cloetingh and Wortel, 1985, 1986). The basement undulations are not symmetrically shaped, but have broad lows and pronounced crests. In the southern parts of the area of intraplate deformation there is negligible sediment thickness. To the north, there is a progressive infill of the undulation lows by the sediments of the Bengal and Nicobar fans (Fig. 1).
Geoid and free-air gravity anomalies contour maps also exhibit undulating character (Figs 1 and 3), correlating with oceanic basement undulations. Folding axes appear to be discontinuous and even seem to undergo rotation across old fracture zones (Bull, 1990; Bull and Scrutton, 1992). The offset of undulations across the fracture zones is consistent with N-S compression. Some rotation is to be expected as the 3-dimensional intraplate stress field is unlikely to be uniformly oriented over this wide area. This is compatible with stress orientations derived from earthquake focal mechanism studies (Bergman and Solomon, 1984,1985; Petroy and Wiens, 1989). Numerical computations of the Indo-Australian plate stress field (Cloetingh and Wortel, 1985, 1986) show how the unique geometry of the plate boundaries and the distribution of dynamic plate boundary processes (collision, subduction, spreading) led to rotated directions of principal stresses with variable magnitudes in the interior of the Indo-Australian plate.
Superimposed on the long wavelength undulations of oceanic basement is intense short wavelength folding and faulting in the crust and overlying sediments. Recent multi-channel seismic profiles (Bull and Scrutton, 1990, 1992; Chamot-Rooke et al., 1993) provide new evidence that the faulted blocks are bounded by high-angle reverse faults penetrating through the crust and possibly into the upper mantle (Fig. 2). Fault activity is recognised on the seismic images by displacements of oceanic basement and sedimentary horizons. Some unreactivated pre-existing basement faults have also been identified, as well as some intra-crustal low-angle faults and sub-horizontal reflectors. The new seismic data also reveals the widespread existence of open anticlinal folds of 5-10 km wavelength within the sedimentary cover, most of them occurring with limited faulting in the deeper parts or with faulting extending from seafloor to basement.

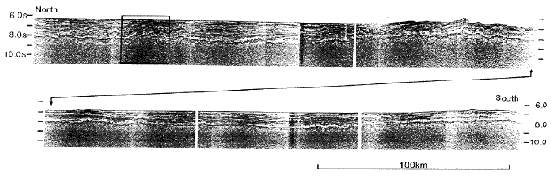
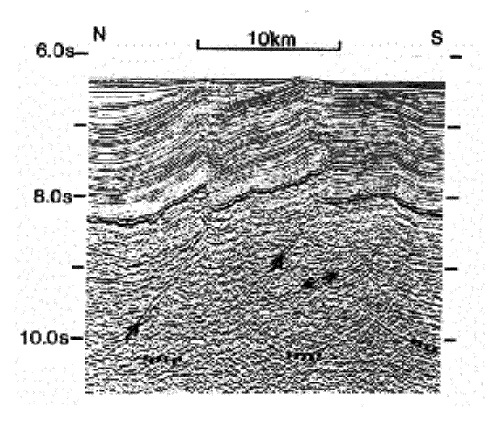
Figure 2. Migrated multichannel seismic reflection profile (from Charles Darwin cruise 28-CD28; Bull and Scrutton, 1990, 1992). Location of the line is displayed in Fig. 1. Reverse faults cutting through the crust are indicated by arrows and possible Moho reflections are highlighted by dots. Vertical scale is in seconds, two-way travel time.

The fault pattern is very complex with variations in fault type, fault dip, dip direction, penetration depth, fault spacing and length, and fault activity. This is, for example, illustrated by the north-south running profile of acoustic basement (Fig. 3), where the small scale effects of varying fault throws are seen to be superimposed on the long wavelength undulations of the oceanic basement. The vast majority of high-angle faults display reverse displacements (Bull and Scrutton, 1990; Pilipenko and Sivukha, 1991). Basement faults can be divided into those that dip 40 to the south, and those that dip 35-40 to the north. If penetrating into the sedimentary cover, faults dramatically steepen (40-90), presumably due to the change in rheology (Melosh, 1990). Some of the N-dipping faults can be resolved to Moho depth (Bull and Scrutton, 1990). The S-dipping faults are less well resolved, as they dip more steeply. Both sets strike 90-100 E, roughly perpendicular to the strike of fracture zones in the area. The fault length averages 10 km, with lengths up to 40 km. Average fault spacing is 5-6 km. The fault amplitude, in terms of the vertical throw of the basement/sedimentary cover interface, averages several hundreds of meters, ranging from very small (detection limit) to over more than 1000 meters (Chamot-Rooke et al., 1993). Some of the basement faults on the seismic profiles seem to penetrate the entire crust and possibly into the subcrustal lithosphere. Bull and Scrutton (1992) suggest that these faults may nucleate in the upper mantle at the brittle-ductile transition and propagate upwards, reactivating the ridge-parallel fault fabric in the oceanic crust.

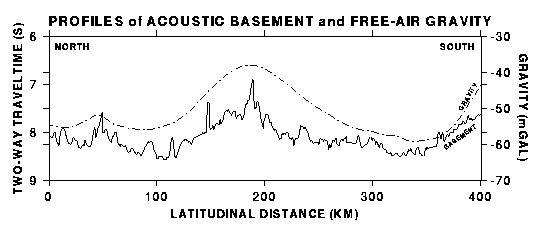
Figure 3. North-south running profiles (for location see Fig. 1) of digitised acoustic basement (solid line) and free-air gravity anomaly (dashed line), demonstrating both spatial modes of tectonic deformation: long wavelength folding and small scale faulting.

These geometrical characteristics, together with other factors, have led to the interpretation that the faults result from the reactivation of the oceanic structural fabric that originated at the midocean spreading centres (Bull, 1990). Steep dipping syn- and antithetic faults are formed in the transition of the rift valley into the rift mountains, creating fault blocks with widths ranging from 1 to 5 km (Macdonald, 1982; Kaz'min and Borisova, 1992). A similar complex fault fabric (in pristine state), although, in general, with lower dips, has also been observed on seismic images of oceanic crust in the Atlantic (White et al., 1990).
Excellent resolution of faults is attributed to the presence of hydrothermal alteration fronts along the fault planes (Shipboard Scientific Party, 1990; Bull and Scrutton, 1992). The hydrothermal activity within the crustal fault blocks is thought to be responsible for the locally anomalous high surface heat flow measured within the intraplate deformation area (Geller et al., 1983; Stein and Weissel, 1990). Regionally, heat flow is normal (as predicted by cooling plate models), indicating that there is no deep thermal origin for the driving mechanism of tectonic deformation. Furthermore, the presence of fluids in the fault planes may have a weakening effect on the frictional resistance against sliding (Brace and Kohlstedt, 1980) and facilitate fault reactivation.
Seismic stratigraphy and DSDP and ODP drilling have demonstrated the presence of two major unconformities within the sediments of the Bengal and Nicobar distal fans over much of the central and northeastern part of the Indian Ocean (Cochran, 1990; Curray and Munasinghe, 1989). An early Eocene (55 Ma) unconformity is correlatable with the first stage of collision of the Indo-Australian plate with the Eurasian plate. A latest Miocene (7 Ma) unconformity has been correlated with the collision of the Indian continent with the Eurasian plate (Peirce, 1978; Patriat and Achache, 1984; Klootwijk et al., 1985; Cochran, 1990; Molnar et al., 1993). The Miocene unconformity separates pre- and syn-deformational sediments, dating the onset of the intraplate deformation at 7 Ma. There is little evidence for deformation before this time. Sedimentary onlap patterns suggest that at 7 Ma there was a major shortening event followed by several smaller pulses of intense fault block rotation and fault motion (Bull and Scrutton, 1992). The relative timing of crustal faulting versus long wavelength folding is unclear, and requires more detailed stratigraphic analysis. Analysis of offset sedimentary horizons shows that on several faults displacement decreases steadily upwards: these faults grow by upwards propagation. Other faults have a roughly constant offset through time, and either formed rapidly at one of the deformation pulses, or are faults on which propagation is complete.
Statistical analysis shows that there is no relationship between magnitude of fault throw and position relative to the long wavelength basement undulations (Bull, 1990). Chamot-Rooke et al. (1993) report a gradual increase in fault throw from south to north over the area of intraplate deformation in the Central Indian Ocean Basin, likely related with the northward increase in sediment loading by the Bengal fan. These authors find for the same area a very long wavelength (600-700 km) trend in fault downthrow direction. The southernmost area is affected primarily by north-dipping faults, the central area by south-dipping faults, whereas the more extensively deformed northernmost area has a mixture of both polarities, although with a majority of north-dipping faults. There is, however, no general relationship between fault downthrow direction and basement undulations (wavelength of 200 km), suggesting a flexural origin for the undulations. In some cases faults tend to downthrow downslope, accentuating the crests of the undulations.
Shortening of this part of the Indo-Australian plate, subject to large compressional stresses, is accommodated by both long wavelength folding and short wavelength faulting and folding. Digitization of oceanic basement from seismic profiles shows that the long wavelength contribution is equivalent to less than 0.1% shortening. Bull and Scrutton (1992) estimate from seismic sections the horizontal shortening due to the reverse faulting to be 1.2 (0.4)%, corresponding to 18 (6)km of shortening over 1500 km north-south extent of deformation. Chamot-Rooke et al. (1993) also assess a possible contribution from very small-scale faulting. Their estimates of the shortening range from 2.5% to maximal 4.3% when small-scale faulting is taken into account. When distributed over the 900 km of deformed basement observed along their seismic profile, these estimates correspond with absolute shortening values of 22 km and 62 km, respectively. At the same longitude, plate tectonic reconstructions (Royer and Chang, 1991) predict a finite shortening of 23 (45)km. Assuming that the shortening has taken place in a steady way from the onset of deformation (7 Ma) until present, corresponding rates of shortening are 2.5 (0.9) mm.a^-1 (Bull and Scrutton, 1992), 3 mm.a^-1 (Royer and Chang, 1991), and 6 (3) mm.a^-1 (Chamot-Rooke et al., 1993). This last rate is consistent with the 6 to 7 mm.a^-1 rate inferred from plate kinematic models (Gordon et al., 1990). The pulselike character of shortening through time, as suggested by the deformation patterns in the sedimentary cover on the seismic profiles, may have led to higher shortening rates at certain times.
Active intraplate deformation is still taking place in the central Indian Ocean, as evidenced by the present-day occurrences of large intraplate earthquakes (Bergman and Solomon, 1980, 1985; Levchenko, 1989; Petroy and Wiens, 1989) and reported substantial micro-seismicity in this area (Levchenko and Ostrovsky, 1993).

A FINITE ELEMENT MODEL

In order to investigate the temporal and spatial relationship between the two modes of tectonic deformation, numerical analyses are carried out using the finite element technique. The numerical analysis assumes a 2-dimensional plane-strain approach, which is validated by the east-west continuity of the axes of the undulations of oceanic basement (Weissel et al., 1980; Bull and Scrutton, 1992). A finite element model (Fig. 4a) is constructed comprising a 2000 km long, N-S section through the central Indian Ocean part of the Indo-Australian plate. To correctly compute displacements, finite elements in the faulted upper part of the plate must be small enough to allow deformation within the faulted blocks, and are therefore sized 1x1 km triangular in the uppermost 10 km, increasing in size to 1x5 km rectangular in the lower parts (Fig. 4b). For the full mesh with dimension 2000x40 km this becomes, including spring elements, 60000 finite elements, connected by more than 42000 nodal points, and with a total of more than 80000 degrees of freedom. Correct behaviour of the elements is ensured by using higher-order elements, in this case linear triangulars and quadrilaterals which have been expanded quadratically using "incompatible modes of deformation" (e.g. Beekman, 1994).

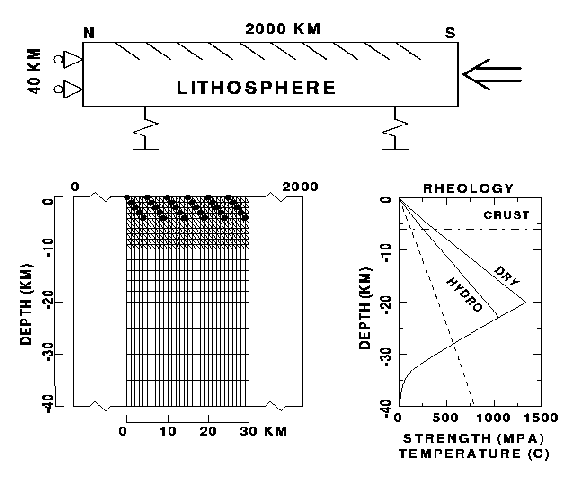
Figure 4. (a) Geometry and boundary conditions of the mechanical model. (b) Enlarged part of the finite element mesh showing geometry of the pre-existing crustal faults. (c) Geotherm (dashed) and yield-strength envelopes (continuous) for a 50 Ma oceanic lithosphere. Assuming hydrostatic pore pressure reduces the strength of the lithosphere.

The complex fault geometry in the oceanic crust is approximated by including a simplified set of faults in the upper part of the plate model, which dip 45 and have a penetration depth and fault spacing of 5 km (average values). For the computations the finite element code TECTON is used (Melosh and Raefsky, 1981), which contains the slippery node technique to model fault behaviour (Melosh and Williams, 1989), and which is modified to also account for friction along fault planes and for elasto-plastic deformation (Beekman, 1994).
The model boundaries are allowed to move freely in both the horizontal and vertical direction, except for the vertical outer edges which are restricted to move horizontally. The vertical buoyancy of the asthenosphere, which can be modelled as a fluid on geological timescales and which counteracts vertical motions of the overlying lithosphere, is included by attaching an array of linear elastic Hookean springs to the base of the plate. The springs will exert forces on the base of the plate, proportional to, but directed opposite to, any vertical deflection of the base of the plate. Horizontal boundary conditions at the N and S edge imitate the effects of the India-Himalayan collision and resistance associated with subduction along the Banda and Sunda arcs, and mid-ocean ridge push, respectively (Cloetingh and Wortel, 1985, 1986). The plate is shortened with a velocity of 6.3 mm.a^-1, according to the currently most accurate available shortening estimate for the area of deformation (Chamot-Rooke et al., 1993). For a 2000 km long plate, this velocity is equivalent to a strain-rate of c. 10^-16 s^-1, which is a value characteristic for the slow deformation of oceanic lithosphere (Carter and Tsenn, 1987). Furthermore, the model is loaded with gravitational body forces.
The Indian oceanic lithosphere comprises a 6 km thick basaltic crust, overlying an olivine upper mantle. The age of the lithosphere in the areas of intraplate deformation in the Indian Ocean varies from 40 Ma in the south to 70 Ma in the north. An average age of 50 Ma is assumed for the entire plate model. The temperatures applied to the model are computed using this model geometry for which an initial steady-state temperature solution can be derived from the heat-conduction equation. Subsequently, the structure is allowed to cool through conduction of heat. Transient temperature fields are computed by solving the heat-conduction equation using a finite difference scheme (3rd order Runge-Kutta). Thermal properties are listed in Table 1. The assumed thermal boundary conditions are a constant surface temperature of 0 ^oC, and an initial surface heatflux of 80 mW.m^-2, which is a characteristic value for young oceanic lithosphere (Sclater et al., 1980). The geotherm after 50 Ma of conductive cooling within the multi-layered oceanic lithosphere is computed for the adopted thermal initial and boundary conditions and plotted in Fig. 4c (dashed line).
The rheological behaviour of the rocks which constitute the lithosphere is derived from laboratory experiments, and subsequently extrapolated to geologically relevant timescales (assuming that the empirically derived rheological laws remain valid). At low confining pressures and low temperatures, brittle failure is predominant. The corresponding frictional yield criterion is given by Byerlee's law (Byerlee, 1978), which can be rewritten in terms of effective principal stress difference, lithostatic overburden pressure, and pore fluid pressure (Ranalli, 1987):

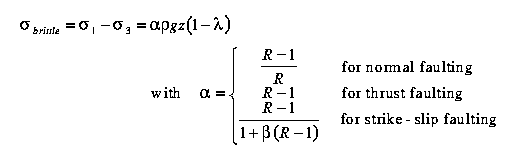(1)

and where sigma₁ and sigma₃ are the maximum and minimum principal stress, respectively, rho is density, g is gravitational acceleration, z is depth, and where

Steady-state creep of a wide variety of rocks is empirically described by a ductile flow law which relates the critical principal stress difference necessary to maintain a given steady-state strain-rate of deformation to a power of the strain-rate, and which, therefore, is called power-law creep (Kirby, 1983):

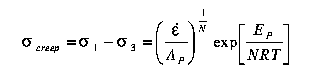(2)

where A_P, N, and E_P are empirically determined material "constants", assumed not to vary with stress and (p,T)-conditions (Ranalli, 1987), and where is the strain-rate. Micro-physically this type of creep mainly involves dislocation climb. The ductile flow law (eqn. 2) shows that the variation of the creep stress with depth is strongly controlled by rock-type and temperature. A steady-state bulk strain-rate of 10^-16 s^-1 is assumed, induced from the applied velocity boundary condition.
Above a critical stress level (200 MPa), power law creep breaks down into high-stress, low-temperature plasticity (dislocation glide), which is phenomenologically described by a Dorn law (Goetze and Evans, 1979; Tsenn and Carter, 1987):

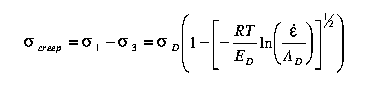(3)

with A_D, E_D, and D material properties, assumed, as before, to be constant.
A depth-varying rheology has been incorporated in the finite element model with elasto-brittle deformation in the upper parts of the oceanic lithosphere and ductile deformation in the lower parts. The associated yield envelope has been constructed using the rheological equation (1) for brittle failure, and equations (2) and (3) for creep flow (at a constant strain-rate of 10^-16 s^-1) of rocks, respectively, and assuming a basaltic crust and a olivine subcrustal lithosphere. Adopted material properties and physical parameters are listed in Table 1. The empirical rheological equations and laboratory derived material properties are used under the assumption they are also valid when extrapolated to geological strain-rates and macroscopic scales. The brittle-ductile transition lies at a depth of 24 km. The depth at which the yield envelope has reduced to an arbitrary small stress level in the order of 10 MPa (Ranalli, 1987) indicates the base of the mechanically strong upper part of the lithosphere, and is used in the modelling to control the depth of the lower boundary of the numerical plate model, here selected at 40 km depth.

TABLE 1. PHYSICAL PARAMETERS AND MATERIAL PROPERTIES¹

DEFINITION	SYMBOL	UNITS	VALUE
gravitational acceleration	g	m.s-2	9.81
universal gas constant	R	J.mole-1.K-1	8.314
seawater density	rhow	kg.m-3	1030
sediment density	rhos	kg.m-3	2200
Moho depth	ZM	km	6
mantle melt temperature	Tm	oC	1300
mantle basal heat flux	qb	mW.m-2	23
static friction coefficient	fs	--	0.6
bulk strain-rate of deformation	epsilon	s-1	10-16
			CRUST	MANTLE
petrology	---	---	basalt	olivine (dry)2
density	rho	kg.m-3	2950	3300
Young's modulus	E	GPa	90	70
Poisson's ratio	nu	---	0.25	0.25
thermal conductivity	k	W.m-1.K-1	3.1	3.5
specific heat	cP	J.kg-1.K-1	1050	1050
power law exponent	N	---	3.05	3.0
power law activation energy	EP	kJ.mole-1	276	510
power law strain rate	epsilonP	Pa-N.s-1	6.31x10-20	7.0x10-14
dorn law activation energy	ED	kJ.mole-1	---	535
dorn law strain rate	epsilonD	s-1	---	5.7x1011
dorn law stress	sigmaD	GPa	---	8.5
FAILURE/CREEP EQUATIONS
brittle failure	sigmabrittle=alpha.rho.g.z(1-lambda)
power law creep	sigmacreep=(epsilon/AP)1/Nexp[EP/NRT]
dorn law creep	sigmacreep=sigmaD{1-[1-(RT/ED)ln(epsilon/AD)]1/2}

¹Sources: Goetze and Evans (1979), Carter and Tsenn (1987), Tsenn and Carter (1987), and Carmichael (1989).
² "dry" refers to rock samples that contain little amounts of structural water

Based on the presence of hydrothermal fluid convection in the upper part of the oceanic lithosphere (Shipboard Scientific Party, 1992) a hydrostatic pore fluid pressure is assumed, which significantly weakens the brittle strength of the lithosphere (equation 1: parameter). Hydrothermal fluid alteration fronts seem to coincide with pre-existing fault planes in the crust, and are thought to lower the frictional resistance against renewed sliding along the fault planes (Brace and Kohlstedt, 1980).
Brittle deformation in the depth range over which the pre-existing faults extend is assumed to be carried out explicitly by these predefined faults. Therefore, no (brittle) yield stress is assigned to the finite elements in this upper part of the plate. Over the remaining depth range down to the brittle-ductile transition there is no information on whether brittle deformation occurs as fracturing of rocks or as fault reactivation. What is known, as evidenced by the existence of deep earthquakes, is that it does occur. Below the resolution depth of the seismic profiles, which is approximately Moho depth, there is no geometrical information of faults (if existing). Therefore, no faults are incorporated at depths exceeding Moho depth. The elements in this depth range are nevertheless characterised by a brittle yield stress assigned on the basis of the empirical brittle deformation equation (1), although any associated brittle failure is modelled numerically as plastic flow (Beekman, 1994).

RESULTS

At time zero the plate undergoes an instantaneous displacement downwards in response to the gravitational loading of the model (see, for example, Fig. 6a). This is followed by a slow linear uplift of the plate surface in response to continuing horizontal shortening. After several million years of shortening (0.3% of shortening occurs in a period of 1 Ma), the models start to develop a folding phase, as illustrated by the evolution of the surface deflection of the plate (Fig. 5a). Fourier spectral analysis of the calculated surface folding demonstrates a dominant wavelength between 200 and 350 km (Fig. 5b).
The folding evolves nonlinearly through time: after several Ma, surface deflections (Fig. 6a) begin to deviate from the homogeneous uplift trend and accelerate upward or downward depending on their position inside a fold (crest or trough). The onset of the deviations corresponds to the onset of lithospheric buckling.
The pre-defined faults in the models exhibit typical stick-slip behaviour through time (Fig. 6b). Jumps in fault slip (at the surface of the plate) are in the order of several meters, accumulating to throws of more than 100 m (Fig. 6b). Comparison of Figs 6a and 6b shows that fault activity starts before the onset of the large scale folding. After long wavelength folding has started to develop, fault activity becomes more complex with some faults exhibiting accelerated reversed faulting, some faults stay locked, and some faults even show normal faulting.
The spatial relationship between long wavelength folding and intensity of faulting is demonstrated by plotting the surface deflection of the plate in combination with the course of the amount of surface fault slip over the plate, both after 8 Ma of shortening (Fig. 7a). In general, maxima in fault throw coincide with fold lows, whereas minima in fault throw coincide with fold highs. This is explained by analysing the fault slip at the plate surface for all faults within the latitudinal distance running from 900 km to 1100 km, which roughly comprises one long-wavelength fold. Figure 7b depicts the surface fault slip for all faults located between 900 km and 1000 km, roughly coinciding with a fold low, and Figure 7c shows the surface fault slip for faults between 1000 km and 1100 km, coinciding with a fold high. All "low positioned" faults exhibit accelerating reverse faulting, thus producing the maxima in fault slip, whereas the "high positioned" faults show fault locking or even an inversion to normal faulting, thus leading to the minima in surface fault slip.

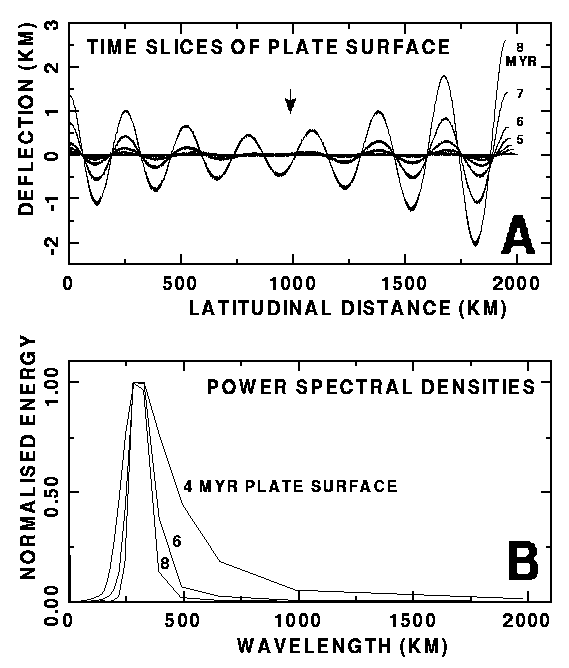
Figure 5. (a) Vertical deflection of the plate model surface through time (1 Ma equals 0.3% shortening). Wavelength of developing folding is in agreement with observations. (b) Normalised Fourier power spectra of the plate surface at several times of loading.

Fig. 8a depicts vertical effective stress profiles inside the plate (at the position denoted by the arrow in Fig. 5a) at several stages of compression. The adopted yield stress envelope limits the effective stresses in the upper brittle and lower ductile part of the lithosphere. In the faulted upper part of the plate, stress profiles develop that have a steeper slope than the theoretical brittle yield envelope. Furthermore, high effective stresses appear at a depth of 5 km (Fig. 8a), which is the depth at which the predefined faults in the model end. The steeper slope, equivalent to a higher "fault reactivation" stress, arises from pre-setting the dip angle of the predefined fault planes. This results, in general, in an angle between fault planes and maximal principal stress that is not the optimal angle for faulting (according to a Mohr diagram) (Jaeger and Cook, 1976). More effective stress is required for reactivation than in the case of an optimal angle on which the yield stress value is based.

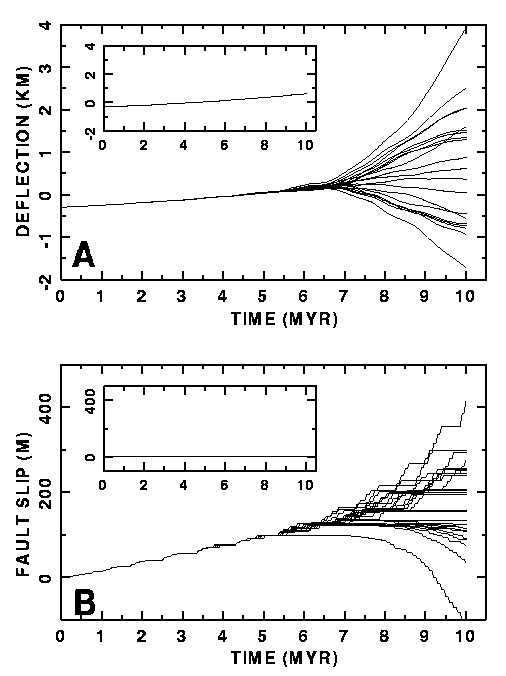
Figure 6. (a) Vertical deflection through time of distinct points at the surface of a horizontally compressed oceanic lithospheric plate with pre-existing faults in its crust. Curves are for surface points separated by a horizontal distance of 50 km. The nonlinear time response is typical for a buckling mode of plate deformation. Inset diagram illustrates behaviour of a plate with locked faults: no buckling. (b) Amount of net slip through time at the surface appearance of a fault. Curves are for every tenth fault (horizontal separation of 50 km). Reverse slip is positive, normal slip is negative. Note the typical stick-slip response. Comparison of Figs 6a and 6b indicates that crustal fault reactivation occurs before lithospheric buckling starts.

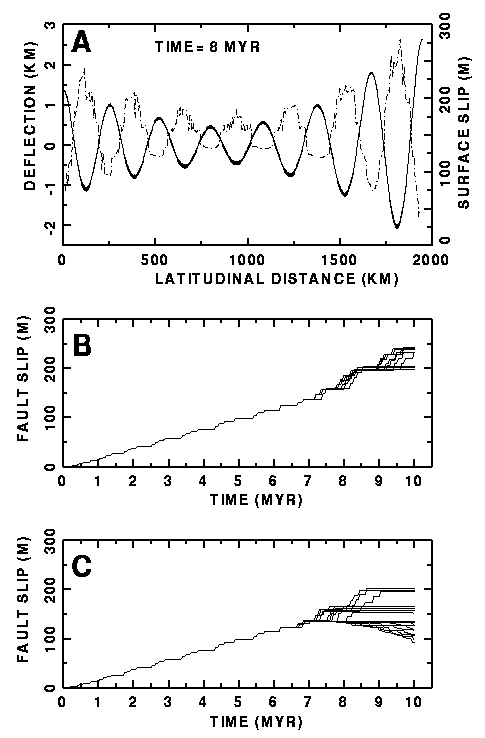
Figure 7. (a) Deflection of the surface of the plate model (continuous line), and the distribution of surface fault slip over the plate (dashed line), both after 8 Ma (=2.4 %) of shortening. (b) Fault slip at the plate surface versus time for all faults located in the long wavelength fold low between 900 km and 1000 km, and (c) for all faults located in the long wavelength fold high between 1000 km and 1100 km.

Fig. 8a depicts vertical effective stress profiles inside the plate (at the position denoted by the arrow in Fig. 5a) at several stages of compression. The adopted yield stress envelope limits the effective stresses in the upper brittle and lower ductile part of the lithosphere. In the faulted upper part of the plate, stress profiles develop that have a steeper slope than the theoretical brittle yield envelope. Furthermore, high effective stresses appear at a depth of 5 km (Fig. 8a), which is the depth at which the predefined faults in the model end. The steeper slope, equivalent to a higher "fault reactivation" stress, arises from pre-setting the dip angle of the predefined fault planes. This results, in general, in an angle between fault planes and maximal principal stress that is not the optimal angle for faulting (according to a Mohr diagram) (Jaeger and Cook, 1976). More effective stress is required for reactivation than in the case of an optimal angle on which the yield stress value is based.
Immediately below the layer which contains the faults effective stresses reach the yield stress limit over an increasingly larger depth range. At depths where this occurs, rocks will deform in a brittle way. Stress also increasingly reaches the yield limit in the lowermost part of the plate model, where rock deformation will occur by ductile flow.
Also illustrated by Fig. 8a is the decrease in thickness of the strong elastic core of the oceanic lithosphere and the associated saturation of the yield envelope, until after c. 8 Ma the elastic core has almost vanished and is not able to mechanically sustain the stresses anymore. The lithosphere starts to fail completely, which will result in extensive deformation, as is numerically indicated by the acceleration of the surface deformation of the plate model and by the increase in magnitude of fault slip (Figs 6a and 6b).
The stick-slip behaviour of faults is also reflected in the temporal fluctuations of effective stress within crustal finite elements (Fig. 8c). Curves are for the first 5 upper-triangular elements in the column below the location denoted by the arrow in Fig. 5a. The "lowest stress" curve belongs to shallowest element (depth range 0-1 km), whereas the "highest stress" curve belongs to the deepest considered element (depth range 4-5 km). Repeated periods of stress buildup are followed by unlocking of the fault and displacement of the fault blocks resulting in stress relaxation. Stress drops associated with the stick-slip fault activity are in the order of a few tens of megapascals. Comparison of stress drops from the same event yields information on propagation direction of fault reactivation. Although not always clearly distinguishable it is possible to recognise downwards propagating stress drop fronts (for example, between 3 and 3.5 Ma) as well as upwards propagating stress drop fronts (e.g. just after 6 Ma), while the event after 8 Ma seems to reactivate the entire fault almost instantaneously. The upwards propagating event, occurring slighly after 6 Ma, starts in the middle of the crust (not originating from a deeper level).
An additional numerical experiment has been undertaken to investigate whether it is indeed the reactivation of the faults, and associated local changes in stress and strain, that ultimately cause the large scale buckling of the plate. To ensure that the faults do not reactivate they have been assigned a very high friction coefficient. Furthermore, the elements in the "faulted" upper part of the plate have now a yield stress, according to the regular yield envelope (Fig. 4c), to avoid this layer behaving as an elastic layer. Thus, failure is still included in this layer with a brittle yield stress derived from the brittle failure equation (1), but the associated deformation is now simulated numerically by plastic flow. The results show that in this case even after 10 Ma of convergence (equivalent to a horizontal shortening of 3%), the initially flat plate is still flat and has not developed a folding mode of deformation. Deflections and power spectra of the plate surface at several times are included in Figs 5a and 5b, but no harmonic deviations are evident. This is also demonstrated by Figs 6a and 6b, where the temporal course of surface point deflection and surface fault slip are shown in the inset diagrams. The slope of the vertical deflection curves in Fig. 6a indicates the homogeneous thickening of the plate in response to the horizontal shortening. Folding/buckling is absent, even when the elastic core of the oceanic lithosphere has almost vanished. This demonstrates that it is the crustal fault reactivation and associated changes in stress and strain, that in these finite element models acts as the perturbing mechanism that facilitates the large scale mode of tectonic deformation.

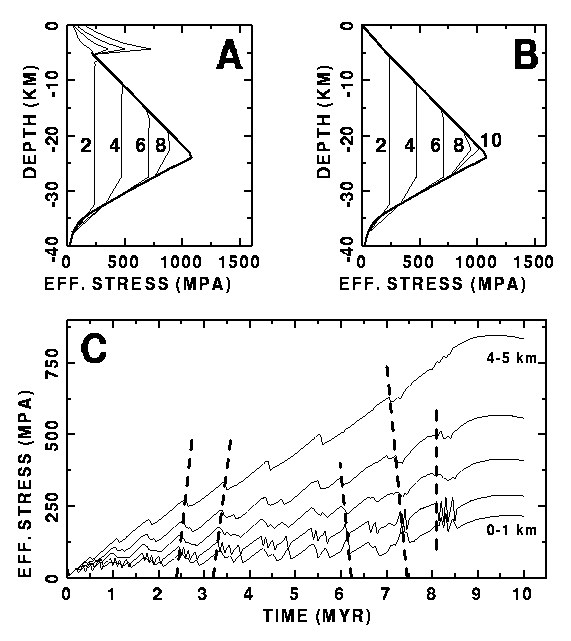
Figure 8. (a) Vertical stress profiles at several stages of compression for the position marked by arrow in Fig. 5a. Solid line is the limiting yield envelope. (b) Same as (a), but now for a plate with locked faults. (c) Effective stress through time in the uppermost five "crustal" upper-triangular finite elements in the column at the location denoted by the arrow in Fig. 5a. The "lowest stress" curve belongs to shallowest element (depth range 0-1 km), whereas the "highest stress" curve belongs to the deepest considered element (depth range 4-5 km). Fault response is typical stick-slip with cycles of stress buildup followed by stress relaxation as the fault becomes active. Lining up stress drops belonging to the same event, shows that activation fronts propagate downwards as well as upwards along a fault plane. Both the stick-slip behaviour and up- and downward propagating reactivation of crustal faults are confirmed by seismic stratigraphic observations.

DISCUSSION

Although quite advanced in the treatment of frictional faulting and the incorporation of a nonlinear depth-varying rheology, the numerical models that have been used are relative simple when considering the complex features and processes within the oceanic lithosphere of the central Indian Ocean. Nevertheless, the models successfully predict stress and strain patterns associated with the long wavelength folding and small scale faulting occurring in this intraplate part of the Indo-Australian plate, which is subjected to considerable compressional stress loading and associated tectonic shortening.
The dominant wavelength of large scale folding that is developed in the models lies well within the range of observed wavelengths in the central Indian Ocean (Zuber, 1987). It is slightly larger than the average observed wavelength, but this can be attributed to the simplified character of the model, not accounting for weakening effects introduced by intra-lithospheric inhomogeneities. The yield envelope, which exerts a major control on the flexural rigidity of the lithosphere, is also a theoretical idealisation, probably resulting in a mechanically too strong lithosphere. The sharp brittle-ductile transition, for example, will probably be transitional, as argued by Carter and Tsenn (1987). Furthermore, recent rock mechanic experiments (Ord and Hobbs, 1989) indicate that the linear brittle branch of the yield envelope may even break down, and maximum sustainable stresses may be as low as 300 MPa, substantially reducing the maximum strength of the lithosphere.
The nonlinear behaviour through time is consistent with the "buckling" response of a horizontally compressed plate, characterised by rapidly accelerating vertical displacements prior to full lithospheric failure (Cloetingh et al., 1989; Stephenson et al., 1990; Stephenson and Cloetingh, 1991). Analysis of vertical effective stress profiles shows that buckling starts when the remaining elastic core of the oceanic lithosphere has almost vanished, as predicted by elasto-plastic plate deformation theory (McAdoo and Sandwell, 1985).
Fault activity starts before the onset of the large scale folding. The increasingly complex activity of the pre-defined faults after long wavelength deformation has started to develop, seems to be caused by an interaction of developing bending stresses with the tectonic compressional stress. Support for this is given by the relationship of fault type and folding magnitude with fault position within a long wavelength fold. Bending would produce additional compressive stress in the downflexed areas and tensile stress in the upflexed areas. These compressive or tensile bending will, respectively, assist or counteract the tectonic stresses. This leads to a decrease in effective stress in upflexed regions, accompanied by permanent locking of faults, or even leads to net tensile effective stresses and normal fault reactivation, as indeed demonstrated by the model results. Statistical analysis of bathymetric and seismic data is required to see if the effects of bending are present.
The pre-defined faults in the models exhibit typical stick-slip behaviour through time. Jumps in fault slip at the plate surface are in the order of several meters, accumulating to throws at the plate's surface of more than 100 m. These values fit with measured fault slips on seismic profiles (Bull and Scrutton, 1992; Chamot-Rooke et al., 1993). The stick-slip fault activity is in agreement with observations of substantial microseismicity in the crust of the central Indian Ocean (Levchenko and Ostrovsky, 1993). Deep earthquakes, which have been observed in this intraplate area (Bergman and Solomon, 1980, 1985), are also correctly predicted by the models with stress within the plate reaching the brittle failure limit over considerable depth ranges down to the brittle-ductile transition (Govers et al., 1992). Reactivation fronts along a single fault can propagate downwards as well as upwards, or reactivate the entire fault instantaneously. Upwards propagating faults and possibly rapidly formed faults have been identified on the seismic stratigraphic record (Bull and Scrutton, 1992). Further analysis is required to check if there are relationships of type of fault reactivation with the position of the fault concerned relative to the long wavelength folds.
The numerical models develop high effective stresses at the tips of the faults. These stress concentrations can be interpreted physically as being responsible for propagation of faults. Such stress concentrations at fault tips are predicted theoretically by the Griffith Crack Theory (Scholz, 1990), and are consistent with rock-mechanics experiments showing that stress concentrations do occur at fault tips (Jaeger and Cook, 1976).
Modelling also shows that no long wavelength mode of tectonic deformation develops when there is no fault activity. This demonstrates that in this study the crustal fault reactivation and associated changes in stress and strain act as the essential perturbing mechanism that facilitates the large scale mode of tectonic deformation.
The complex fault fabric in the Indian Ocean crust has been approximated by a simplified set of faults with a geometry based on average values. Additional numerical analyses have to be carried out to investigate if variations in one or more of the fault parameters (such as dip, dip direction, penetration depth) have a major influence on the long wavelength deformation of the Indian Ocean lithosphere. The successful predictions of the numerical model with the "average" fault set do suggest, however, that it is merely the reactivation of faults that is of essential importance rather than the geometrical features of the faults.
Another model simplification which may affect the model results is the assumption of a constant lithospheric thermal age (and thus lithospheric thickness) for the entire model, whereas the the thermal age of the area of interest ranges from approximately 40 Ma in the south to 70 Ma in the north. The increase in age is probably to gradual to initiate the intraplate deformation. It may, however, affect the wavelength of the large scale folding, as with age also the flexural rigidity of the lithosphere increases, which will lead to a larger wavelength of deformation (McAdoo and Sandwell, 1985). Zuber (1987) indeed observed a gradual northward increase in the wavelength of lithospheric folding in the central Indian Ocean.

CONCLUSIONS

Substantial compressional stresses in the central Indian Ocean reactivate pre-existing crustal faults, and, in a later phase, initiate folding and buckling of the entire oceanic lithosphere. Stress and strain patterns, spatial as well as temporal, are successfully predicted by the numerical models, and are in agreement with geophysical observations.
The modelling also demonstrates that in the absence of fault reactivation no lithospheric folding develops. Crustal fault reactivation, therefore, appears to be essential to facilitate long-wavelength oceanic lithospheric buckling in the central Indian Ocean.

ACKNOWLEDGEMENTS

We thank G. Ranalli and R.A. Stephenson for their constructive reviews of an early draft of this paper. Comments by F. Nieuwland and an anonymous reviewer are also gratefully acknowledged. This is NSG publication 950408.

REFERENCES

• Beekman, F., Tectonic modelling of thick-skinned compressional intraplate deformation, PhD thesis, Vrije Universiteit, Amsterdam, 152 pp., 1994.
• Bergman, E. A., and S. C. Solomon, Oceanic intraplate earthquakes: Implications for local and regional intraplate stress, J. Geophys. Res., 85, 5389-5410, 1980.
• Bergman, E. A., and S. C. Solomon, Source mechanisms of earthquakes near mid-ocean ridges from body waveform inversion: Implications for the early evolution of oceanic lithosphere, J. Geophys. Res., 89, 11,415-11,441, 1984.
• Bergman, E. A., and S. C. Solomon, Earthquake source mechanisms from body waveform inversion and intraplate tectonics in the northern Indian Ocean, Phys. Earth Planet. Inter., 40, 1-23, 1985.
• Brace, W.F., and D.L. Kohlstedt, Limits on lithospheric stress imposed by laboratory experiments, Journal of Geophysical Research, 85(B11), 6248-6252, 1980.
• Bull, J.M., Structural style of intra-plate deformation, Central Indian Ocean Basin: evidence for the role of fracture zones, Tectonophysics, 184, 213-228, 1990.
• Bull, J.M., and R.A. Scrutton, Fault reactivation in the central Indian Ocean and the rheology of oceanic lithosphere, Nature, 344, 855-858, 1990.
• Bull, J.M., and R.A. Scrutton, Seismic reflection images of intraplate deformation, central Indian Ocean, and their tectonic significance, Journal of the Geological Society, London, 149, 955-966, 1992.
• Bull, J.M., J. Martinod, and Ph. Davy, Buckling of the oceanic lithosphere from geophysical data and experiments, Tectonics, 11, 537-548, 1992.
• Byerlee, J. D., Friction of rocks. Pure and Applied Geophysics, 116, 615-626, 1978.
• Carmichael, R.S., Practical handbook of physical properties of rocks and minerals , 741 pp. CRC Press, Boca Raton, Florida, 1989.
• Carter, N.L., and M.C. Tsenn, Flow properties of continental lithosphere, Tectonophysics, 136, 27-63, 1987.
• Chamot-Rooke, N., F. Jestin, B. de Voogd, and Phedre Working Group, Intraplate shortening in the central Indian Ocean determined from a 2100-km-long north-south deep seismic reflection profile, Geology, 21, 1043-1046, 1993.
• Cloetingh, S., and R. Wortel, Regional stress field of the Indian Plate, Geophys. Res. Lett., 12, 77-80, 1985.
• Cloetingh, S., and R. Wortel, Stress in the Indo-Australian plate, Tectonophysics, 132, 49-67, 1986.
• Cloetingh, S., H. Kooi, and W. Groenewoud, Intraplate stress and sedimentary basin evolution, in Origin and evolution of Sedimentary Basins and their energy and mineral resources, AGU Geophysical Monograph 48, edited by R.A. Price, pp. 1-16, 1989.
• Cochran, J.R., Himalayan uplift, sealevel and the record of the Bengal Fan sedimentation at the ODP Leg 116 Sites, in Proc. ODP Sci. Results, 116, edited by J.R. Cochran, D.A.V. Stow, et al, pp. 397-414, College Station, Texas, 1990.
• Curray, J.R., and D.G. Moore, Growth of the Bengal Deep-Sea Fan and Denudation in the Himalayas, Geol. Soc. Am. Bull., 82, 563-572, 1971.
• Curray, J.R., and T. Munasinghe, Timing of intraplate deformation, northeastern Indian Ocean, Earth Planet. Sci. Lett., 94, 71-77, 1989.
• DeMets, C., R.G. Gordon, D.F. Argus, and S. Stein, Current plate motions, Geophys. J. Int, 101, 425-478, 1990.
• Geller, C. A., J. K. Weissel, and R. N. Anderson, Heat transfer and intraplate deformation in the central Indian Ocean, J. Geophys. Res., 88, 1018-1032, 1983.
• Goetze, C. & Evans, B., Stress and temperature in the bending lithosphere as constrained by experimental rock mechanics. Geophysical Monograph, 59, 463-478, 1979.
• Gordon, R.G., C. DeMets, and D.F. Argus, Kinematic constraints on distributed lithospheric deformation in the equatorial Indian Ocean from present motion between the Australian and Indian plates, Tectonics, 9(3), 409-422, 1990.
• Govers, R., M.J.R. Wortel, S.A.P.L. Cloetingh, and C.A. Stein, Stress magnitude estimates from earthquakes in oceanic plate interiors, J. Geophys. Res., 97(B8), 11,749-11,760, 1992.
• Jaeger, J. C., and N. G. W. Cook, Fundamentals of Rock Mechanics, Chapman and Hall, London, 1976.
• Karner, G.D., and J.K. Weissel, Factors controlling the location of compressional deformation of oceanic lithosphere in the central Indian Ocean, J. Geophys. Res., 95(B12), 19,795-19,810, 1990.
• Kaz'min, V.G., and I.A. Borisova, Mechanisms of rift valley formation for slowly spreading ridges, Geotectonics, 26(4), 344-352, 1992.
• Kirby, S. H., Rheology of the lithosphere. Reviews of Geophysics and Space Physics, 21, 1458-1487, 1983.
• Klootwijk, C.T., P.J. Conaghan, and C. McA. Powell, The Himalayan Arc: large-scale continental subduction, oroclinal bending and back-arc spreading, Earth Planet. Sci. Lett., 75, 167-183, 1985.
• Leger, G.T., and K.E. Louden, Seismic refraction measurements in the Central Indian Basin: Evidence for crustal thickening related to intraplate deformation, in Proceedings of the Ocean Drilling Program, Scientific Reports, 116, edited by J.R. Cochran, and D.A.V. Stow, 1990.
• Levchenko, O.V., Tectonic aspects of intraplate seismicity in the northeastern Indian Ocean, Tectonophysics, 170, 125-139, 1989.
• Levchenko, O.V., and A.O. Ostrovsky, Seismic seafloor observations: A study of "anomalous" intraplate seismicity in the northeastern Indian Ocean, Phys. Earth Planet. Inter., 74, 173-182, 1993.
• Macdonald, K.C., MID-OCEAN RIDGES: Fine scale tectonics, volcanic and hydrothermal processes within the plate boundary zone, Ann. Rev. Earth Planet. Sci., 10, 155-190, 1982.
• Martinod, J., and P. Davy, Periodic instabilities during compression or extension of the lithosphere, 1. Deformation modes from an analytical perturbation mode, J. Geophys. Res., 97(B2), 1999-2014, 1992.
• McAdoo, D. C., and D. T. Sandwell, Folding of oceanic lithosphere, J. Geophys. Res., 90, 8563-8569, 1985.
• Melosh, H.J., Mechanical basis for low-angle normal faulting in the Basin and Range Province, Nature, 343, 331-335, 1990.
• Melosh, H.J., and A Raefsky, A simple and efficient method for introducing faults into finite element computations, Bull. Seism. Soc. Am., 71, 1391-1400, 1981.
• Melosh, H.J., and C.A. Williams, Jr., Mechanics of graben formation in crustal rocks: A finite element analysis, J. Geophys. Res., 94(B10), 13,961-13,973, 1989.
• Molnar, P., Ph. England, and J. Martinod, Mantle dynamics, uplift of the Tibetan Plateau, and the Indian monsoon, Reviews of Geophysics, 31(4), 357-396, 1993.
• Neprochnov, Y.P., O.V. Levchenko, L.R. Merklin, and V.V. Sedov, The structure and tectonics of the intraplate deformation area in the Indian Ocean, Tectonophysics, 156, 89-106, 1988.
• Ord, A., and B.E. Hobbs, The strength of the continental crust, detachment zones and the development of plastic instabilities, Tectonophysics, 158, 269-289, 1989.
• Patriat, P., and J. Achache, India-Eurasia collision chronology has implications for crustal shortening and driving mechanism of plates, Nature, 311, 615-621, 1984.
• Peirce, J. W., The northward motion of India since the Late Cretaceous, Geophys. J. R. astron. Soc., 52, 277-311, 1978.
• Petroy, D.E., and D.A. Wiens, Historical seismicity and Implications for Diffuse Plate Convergence in the Northeast Indian Ocean, J. Geophys. Res., 94(B9), 12,301-12,319, 1989.
• Pilipenko, A.I., and N.M. Sivukha, Geological structure and geodynamics of the West Australian Basin (Wharton Basin), Geotectonics, 25(1), 84-93, 1991.
• Ranalli, G., Rheology of the Earth. Deformation and flow processes in geophysics and geodynamics. 386 pp.Allen & Unwin, Boston, 1987.
• Royer, J.-Y., and T. Chang, Evidence for relative motions between the Indian and Australian Plates during the last 20 m.y. from plate tectonic reconstructions: implications for the deformation of the Indo-Australian Plate, Journal of Geophysical Research, 96(B11), 11,779-11,802, 1991.
• Sandwell, D.T., and W.H.F. Smith, Global marine gravity from ERS-1, Geosat, and Seasat reveals new tectonic fabric, EOS, 73(43), Supplement, 1992 Fall Meeting, 1992.
• Scholz, C., The Mechanics of Earthquakes and Faulting, 439 pp., Cambridge University Press, Cambridge, 1990.
• Sclater, J. G., Jaupart, C. & Galson, D., The heat flow through oceanic and continental crust and the heat loss of the Earth, Reviews of Geophysics and Space Physics, 18, 269-311, 1980.
• Shipboard Scientific Party, ODP Leg 116 Survey, in Proceedings of the Ocean Drilling Program, Scientific Reports, 116, edited by J.R. Cochran, and D.A.V. Stow, 1990.
• Stein, C.A., and J.K. Weissel, Constraints on the Central Indian Basin thermal structure from heat flow, seismicity and bathymetry, Tectonophysics, 176, 315-332, 1990.
• Stein, C.A., S. Cloetingh, and R. Wortel, SEASAT-derived gravity constraints on stress and deformation in the northeastern Indian Ocean, Geophys. Res. Lett., 16(8), 823-826, 1989.
• Stephenson, R.A., and S. Cloetingh, Some examples and mechanical aspects of continental lithosphere folding, Tectonophysics, 188, 27-37, 1991.
• Stephenson, R.A., B.D. Ricketts, S.A.P.L. Cloetingh, and F. Beekman, Lithosphere folds in the Eurekan Orogen, Arctic Canada?, Geology, 18, 103-106, 1990.
• Timoshenko, S.P., and S. Woinowsky-Krieger, Theory of Plates and Shells, 2nd edition, 580 pp., McGraw-Hill, Singapore, 1959
• Tsenn, M.C. & Carter, N.L., Upper limits of power law creep of rocks. Tectonophysics, 136, 1-26, 1987.
• Verzhbitsky, E.V., and L.I. Lobkovsky, On the mechanism of heating up the Indo-Australian plate, Journal of Geodynamics, 17(1/2), 27-38, 1993.
• Weissel, J. K., R. N. Anderson, and C. A. Geller, Deformation of the Indo-Australian plate, Nature, 287, 284-291, 1980.
• White, R.S., R.S. Detrick, J.C. Mutter, P. Buhl, T.A. Minshull, and E. Morris, New seismic images of oceanic crustal structure, Geology, 18, 462-465, 1990.
• Zuber, M.T., Compression of the oceanic lithosphere: An analysis of intraplate deformation in the Central Indian Basin, J. Geophys. Res., 92(B6), 4817-4825, 1987.

Address

Institute of Earth Sciences, Vrije Universiteit
De Boelelaan 1085
1081 HV Amsterdam
The Netherlands

Phone: +31-20-4449801
Fax: +31-20-4449943

beef@geo.vu.nl

Return to my home page