Van Westrenen, W., Blundy, J.D. and Wood, B.J. (1999a) Crystal-chemical controls on trace element partitioning between garnet and anhydrous silicate melt. Am. Min. 84, 838-847. Copyright © Mineralogical Society of America.

We have performed experiments at 3.0 GPa and 1530-1565 ° C to investigate the effects of crystal composition on trace element partitioning between garnet and anhydrous silicate melt. Bulk compositions along the pyrope (Mg3Al2Si3O12)-grossular (Ca3Al2Si3O12) join, doped with a suite of trace elements (Li, B, K, Sc, Ti, Sr, Y, Zr, Nb, Cd, In, REE, Hf, Ta, Th and U) produced homogeneous garnets, ranging in composition from Py84Gr16 to Py9Gr91, in equilibrium with melt.

Trace element partition coefficients (D’s), measured by SIMS, depend greatly on the Mg / (Mg + Ca) of garnet. For example, from Py₈₄ to Py₉ DLa increases from 0.004 to 0.2, while DU increases from 0.029 to 0.42. These variations can be explained by the lattice strain model of Blundy and Wood (1994), which describes trace element partitioning of an element i in terms of the ionic radius of i (ri), the size of the lattice site on which i partitions (r0), the Young’s modulus of the site (E), and the (theoretical) partition coefficient D0 for an ion of radius r0.

For trivalent cations substituting in the garnet X-site (Y, REE, Sc, In), apparent values of r0 fitted to our data vary systematically from 0.935 ± 0.004 Å (Py84) to 0.99 ± 0.01 Å (Py9), a trend consistent with variations in the size of the X-site. Values of D0 show an increase from Py9 (D0 = 2.8 ± 0.1) to Py84 (4.8 ± 0.1) and Young’s modulus E varies from 257 ± 20 GPa for Py60 to 590 ± 40 GPa for Py84. These results allow a quantitative assessment of the influence of crystal chemistry on garnet-melt D’s, thereby forming the basis for a predictive model similar to that recently developed for clinopyroxene-melt partitioning by Wood and Blundy (1997). Our new data emphasise the importance of taking into account crystal composition when modelling trace element behaviour in natural systems.

Several lines of geochemical evidence, such as U-Th isotopic disequilibrium and Sm-Nd and Lu-Hf isotope systematics in MORB, point towards an important role for garnet in the mantle melting region (e.g., Salters and Hart 1989; Beattie 1993; LaTourrette et al. 1993; Salters 1996). The evidence supporting this interpretation is largely based on the ability of garnet to incorporate certain trace elements preferentially over others, as derived from a limited number of high-pressure, high-temperature partitioning experiments. In fact, all of the existing geochemical models of mantle melting are predicated on assumptions about differences in partitioning behaviour between garnet and clinopyroxene, assumptions which have been called into question recently (Blundy et al. 1998). Since the existing garnet/melt partitioning data set does not cover a wide range in pressure (P), temperature (T) and bulk composition (X), it is impossible to take account of the effects of these intensive parameters on garnet-melt partition coefficients during the melting process. Most geochemical models are, therefore, based on fixed, constant garnet/melt partition coefficients measured under one set of ‘appropriate’ conditions. This approach, as shown by Blundy and Brodie (1997), can cause large errors in modelling of mantle melting processes.

There is, therefore, a need for systematic studies of garnet/melt partitioning, isolating where possible the effects of P, T, X (and fO₂ in the case of polyvalent cations). The purpose of this study was to determine specifically the role that crystal chemistry plays in controlling the partitioning between garnet and anhydrous silicate melt. Experiments were performed in the simple system CaO-MgO-Al2O3-SiO2 (CMAS) under isobaric (3.0 GPa), near-isothermal (1530-1565 oC) conditions to isolate the effect of Mg / (Mg + Ca) ratio. We show for the first time a systematic dependence of D’s on garnet composition along the pyrope-grossular join. Although our experiments were performed in a simple system, our results have important implications for future models of garnet/melt partitioning applicable to natural systems.

Starting materials with compositions Mg3Al2Si3O12 and Ca3Al2Si3O12 were prepared by mixing appropriate proportions of analytical grade oxides (for Mg, Al and Si) and carbonate (for Ca). The pyrope oxide mix was first heated in a Pt crucible from 800-1300 oC, then ground under ethanol in an agate mortar previously used for Fe-free materials only. The grossular mix was twice heated slowly from 650-1300 oC (ground under ethanol after each heating cycle) to ensure full decarbonation. Subsequently both starting mixes were heated at 1300 oC for 24 h to remove any remaining adsorbed water and CO2. In order to re-create the garnet/melt relations at 3.0 GPa reported by Walter and Presnall (1994) and Maaløe and Wyllie (1979) we then prepared the following mixtures: Py₈₂Gr₁₈ (mixture G1); Py50Gr50 (G3); and Py15Gr85 (G4). In addition, a mixture G2 was prepared with a composition close to the melt composition generated by Walter and Presnall (1994) in their experiment 562-1.

1000 ppm Atomic Absorption standard solutions were used to dope mixtures G2, G3 and G4 with a suite of 26 trace elements (see Table 2.1 for details) chosen so as to minimise molecular interferences in ionprobe analysis. Total dopant levels were limited to 0.14-0.51 wt% (Table 2.1). After drying at room temperature all doped mixtures were kept at 110 oC until use.

The experimental arrangement is shown in Figure 2.1. All samples were loaded into graphite capsules fitted tightly inside 2 mm O.D. Pt capsules. To assess the influence of the graphite liner, one experiment was performed in a Pt capsule only (see Table 2.2). Before welding, all capsules were held at 760 oC for 10 min to drive off any adsorbed water. The welded capsule was then embedded in a crushable alumina cylinder and covered with a thin Pt disk to protect it from the W-3%Re/W-25%Re thermocouple. Surrounding parts consist of a graphite furnace, a silica glass inner sleeve to increase quench rates and a BaCO3 outer sleeve. The vertical temperature gradient across the capsule is on the order of 10 ^oC (Frost and Wood 1997).

Figure 2.1. Experimental setup - see text for details. t/c is W-3%Re / W-25%Re thermocouple.

A pressure calibration was performed for this cell. 50:50 mixtures of pyrope and enstatite, plus 3 wt% PbO flux, were run at nominal pressures of 2.5-3.3 GPa and temperatures of 1300-1600 oC. Measured Al2O3 contents of resulting enstatite were compared with data of Perkins III et al. (1981). The resulting pressure correction at our run temperatures is –13 ± 1%. No correction was made for the dependence of thermocouple emf on pressure. During heating to run temperature pressure was increased continuously, the last increment of pressure being applied after the run temperature had been reached (hot-piston-in technique). Experimental conditions and durations are shown in Table 2.2.

Major element compositions of starting materials and experimental products were determined with the JEOL 8600 Superprobe at Bristol University, using an accelerating voltage of 15 kV and a beam current of 15 nA. A focused beam with a 1 m m spot size was used for garnet analyses, while a defocused beam (spot size 10 m m) was used for analyses of quench crystals and glass. Counting times were 30 seconds for all four elements. Standards used were wollastonite for Si and Ca, spinel for Al and olivine for Mg. Analyses of secondary standards (including diopside, KK1 kaersutite, Kakanui garnet and natural pyrope) were consistently within 2s of published values.

Trace elements were measured on Au-coated mounts with the Cameca IMS-4f ion microprobe at Edinburgh University. The primary beam was 10.69 kV O- ions with 8-10 nA beam current, focused to a ~ 20 m m spot. To reduce transmission of molecular ion species an offset of 73 ± 20 eV was applied to the secondary ion accelerating voltage of 4.5 keV. The energy window was set to 20 eV. Isotopes 7Li, 11B, 41K, 42Ca, 44Ca, 45Sc, 47Ti, 88Sr, 89Y, 90Zr, 93Nb, 114Cd, 115In, 139La, 141Pr, 149Sm, 159Tb, 167Er, 169Tm, 172Yb, 175Lu, 178Hf, 181Ta,232Th and 238U were measured and ratioed to 30Si, after calibration on NIST standard SRM610. Mass 130.5 was used to monitor background - all analyses reported here have zero background counts. Counting times were adjusted so as to obtain at least 103 total counts per isotope and were typically (for analyses consisting of 10 cycles) around 5 seconds per cycle for elements present at the ppm level.

Accuracy of the SIMS analyses was assessed by regularly analysing a set of secondary standards: basalt glasses BIR-1 (Jochum et al. 1990) and BCR-1 (Govindaraju 1994), Irving and Frey (1978) garnet DD1, and Mongolian garnet MU5388 (Norman et al. 1996). Table 2.3 and Figure 2.2 compare published trace element compositions with values measured by us over a period of 4 years. Figure 2.2 shows accuracy for all elements is generally better than 15% and better than 10% for most REE. More importantly, where available for both garnet and glass standards, observed/published ratios overlap within error for all elements except Sr, Y and La (for a discussion of these exceptions see legend of Fig. 2.2). The absence of differential matrix effects for glass relative to garnet means the accuracy of our calculated partition coefficients is better than the percentages given above.

In addition to the regular analysis of secondary standards mentioned above, we are involved in the development of a set of four new garnet trace element standards using SIMS and LA-ICP-MS. Details of these measurements are given in Appendix 1.

Figure 2.2. Comparison of observed and published values for secondary garnet/glass standards. Data taken from Table 2.3. Deviation of La in DD1 caused by very low concentration (0.03 ppm according to Irving and Frey 1978), close to the detection limit of the ionprobe. Observed / published ratio (Obs / Pub) for Sr is always higher in garnet standards than in glass standards, implying our Sr partition coefficients might be overestimated. (Obs / Pub) data for Y in glass BIR-1 is lower than (Obs / Pub) in glass BCR-1. This might be caused by a small error in published Y content of BIR-1 (Jochum et al. 1990). All our analyses were calibrated against NIST recommended values for SRM610.

Experimental products and their major and trace element compositions are listed in Tables 2.2 and 2.4, respectively. All experiments produced several homogeneous garnets with a maximum diameter of about 30 m m. Experiments 8 and 11 produced minor orthopyroxene (< 5 m m in diameter - unsuitable for SIMS analysis). Experiment 11 (see Fig. 2.3) produced both glass and quench crystals, while all other runs produced quench crystals only. Figure 2.3 illustrates the spinifex texture of the quench crystals. Major and trace element compositions of glass and quench crystals in experiment 11 are indistinguishable, except for boron which is significantly higher in the latter. This is probably due to surface contamination in the cracks between the quench crystals and in this case, values from the glass were used to calculate D. We observed no significant heterogeneity in any of our garnet or quench phases for any of the trace elements, as illustrated by the small relative errors given in Table 2.4.

Figure 2.3. Back-scattered electron photomicrograph of experiment 11 showing garnet (Gt), quench (Q), glass (G), gold coating (Au) and ionprobe pits (IP). Width of view 350 m m.

Experiments 8 and 11 were performed at very similar conditions and using the same starting material, but the Pt capsule in experiment 8 was not graphite-lined. Direct comparison between the experiments is hampered for some elements by the influence of small amount of surface and/or glass contamination in some garnet analyses (e.g. B, Li, Sr and La, see later discussion). Inhomogeneity of the starting material for some elements (K, Zr and Th), which had to be doped to high levels, manifests itself in relatively large differences in absolute concentrations between the two experiments, although in the case of Zr and Th calculated partition coefficients are virtually the same. For other elements (Cd, Ta, In and Nb) it is obvious from anomalously low concentrations in the quench phase that alloying with the Pt capsule has taken place in experiment 8 (Note that In and Nb were completely lost from this experiment and are therefore absent from Table 2.4). Partition coefficients calculated for experiment 8 for K, Cd, Ta, In and Nb are, hence, not included in Table 2.5. On the other hand, agreement between the REE data for experiments 8 and 11 is very good, warranting the inclusion of REE partitioning data for experiment 8 in later discussion.

Major element compositions of the garnets span a large part of the pyrope-grossular join, ranging from Py9Gr91 (experiment 13) to Py84Gr16 (experiment 11). Calculated garnet/melt partition coefficients (Table 2.5) are summarised in Figure 2.4a, showing the large variation in D along the join. As expected, partition coefficients for Py60 and Py65 are very similar, as are D’s for Py₈₂ and Py₈₄. More importantly, partition coefficients for highly incompatible elements such as LREE, Sr and Li vary by more than 2 orders of magnitude along the join from Py84 to Py9. On the other hand, HREE like Yb and Lu show relatively little variation with garnet composition. The existing garnet-melt partitioning data do not cover a wide enough range in garnet composition to observe these effects.

However, Harte and Kirkley (1997), in their study of eclogite xenoliths from the Roberts Victor kimberlite pipe in South Africa, provide data on garnet-clinopyroxene partition coefficients (D^Gt/Cpx) as a function of garnet composition in the range from Gr₈ to Gr₅₀. They observe an increase by up to three orders of magnitude in D^Gt/Cpx(LREE) with increasing grossular content, while D^Gt/Cpx(HREE) remains approximately constant.

Figure 2.4. (a) Spidergram showing garnet / melt partition coefficients from this study. Order of elements along x-axis where possible from Sun and McDonough (1989), In and Li after Withers (1997). Note large variation in D’s with garnet composition for some elements (e.g. LREE, Sr, Li, HFSE). (b) Variation of DU / DTh and CPP (Critical Partitioning Parameter - Hart and Dunn 1993) along pyrope-grossular join. Error bars are 1s .

This is consistent with our experimental results (Fig. 2.4a). Several trace elements listed in Table 2.5 have not been used before in garnet-melt partitioning studies. Li is consistently more incompatible than the HREE, confirming the expectations of Ryan and Langmuir (1987). Figure 2.4a also shows that indium is compatible in garnet (DIn ~ 2), while DCd is about unity for most experiments. Boron is highly incompatible, with DB similar to DLa (Table 2.5). Finally, Pr is incompatible with DLa < DPr < DSm.

Parameters deemed important for mantle melting also show remarkable variation along the pyrope-grossular join: Figure 2.4b shows the large change in DU / DTh with garnet composition (from 4.1 for Py84 to only 1.3 for Py9). Values for the Critical Partitioning Parameter (CPP = [DSm × DHf] / [DNd × DLu]) from Hart and Dunn (1993) are also shown in Figure 2.4b. CPPs give a measure of the extent of fractionation of the Sm/Nd and Lu/Hf isotopic systems, and the fact that mantle garnets have a low CPP has been used to infer MORB melting needs to start in the garnet lherzolite stability field (e.g. Salters and Hart 1989). The CPPs for Py82 and Py84 are very close to the value of 0.18 used by Salters (1996) in his modelling of MORB generation. However, other garnets show values much closer to or even greater than 1, similar to the value calculated for the garnet from the experiment of Hauri et al. (1994; CPP = 0.97) and, more significantly, similar to CPP values for clinopyroxene (Blundy et al. 1998).

To interpret the compositional dependence of trace element partitioning seen in Figure 2.4, we use the crystal-melt partitioning model of Blundy and Wood (1994), as extended by Wood and Blundy (1997). This model is based on the long-established observation (e.g. Onuma et al. 1968) that mineral-melt partition coefficients for series of isovalent cations show a near-parabolic dependence on cation radius. This has been shown for plagioclase (Blundy and Wood 1991), amphibole (e.g., Liu et al. 1992; LaTourrette et al., 1995; Brenan et al., 1995), clinopyroxene (Blundy et al. 1995; Wood and Blundy 1997), olivine (Beattie 1994) and garnet (Liu et al. 1992; Van Westrenen et al. 1997; Withers 1997). Beattie (1994) and Blundy and Wood (B&W, 1994) explained these observations using lattice strain models, based on the work of Nagasawa (1966) and Brice (1975), respectively. In the B&W model, trace element partitioning on a given structural site is characterised by the site radius (r0), its Young’s modulus (E) and the (theoretical) strain-free partition coefficient D0 for an element with ‘ideal’ radius r0:

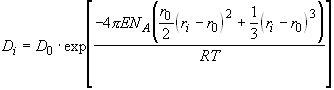(2.1)

NA is Avogadro’s number, R is the gas constant and T is in K. Wood and Blundy (1997) used this model to predict REE D’s for clinopyroxene-melt partitioning, and Van Westrenen et al. (1997) concluded from a study of available literature data that this model is also applicable to garnet-melt partitioning of trace elements.

We used a Levenberg-Marquardt-type non-linear least-squares fitting routine (Press et al. 1992) to derive best-fit values for r0, D0 and E for partitioning of the large (ri ³ 0.89 Å) 3+ cations (REE, Y, In and Sc). Trivalent cations were chosen as the basis of these fits since these form the largest group of isovalent trace elements in our experiments. Their D’s should therefore provide the tightest constraints on partitioning behaviour. Standard deviations of multiple analyses from Table 2.5 were used to weight the fits. The following additional constraints and assumptions were applied:

· The REE and Y all partition exclusively into the garnet X-site. Recent EXAFS studies (Quartieri et al. 1997) and initial studies of garnet/melt partitioning (Van Westrenen et al. 1997; Withers 1997) support this assumption.

· Indium can be univalent or trivalent. Since garnet-melt partition coefficients for 1+ cations (K and Li) are about 2 orders of magnitude smaller than D’s for 3+ cations (see Fig. 2.4a), small amounts of In1+ should lead to a significant lowering of observed D(In) relative to a 3+ ion of the same radius. Fitted values for D(In3+) should therefore generally be higher than observed D(In).

· Sc can enter both the garnet X- and Y-sites (e.g., Geller 1967). Sc entering the Y-site has been observed by several authors (see Geller 1967), but because of its ionic radius (0.89 Å according to Shannon 1976), and in the absence of other (e.g., EXAFS) data, we expect some of the Sc to enter the X-site. With Sc entering both sites, fitted D(Sc) should underestimate the observed D(Sc).

Table 2.6 gives our best-fit values for r0, D0 and E. Plots of ionic radius versus D using these parameters (Fig. 2.5) show good agreement between observation and model for all experiments, bearing in mind the assumptions listed above. Deviations of our fitted values from the measured partition coefficients for La and Pr are probably caused by slight (~ 0.5%) contamination of garnet by glass during SIMS analysis.

Figure 2.5. (a) Onuma diagram for experiment 8 showing partition coefficients for trivalent cations entering the garnet X-site, together with non-linear weighted least-squares fits to Eqn. 2.1. Error bars (shown if bigger than symbols) are 1s .

Figure 2.5. (b - c) Onuma diagrams for experiments 11 and 12 showing partition coefficients for trivalent cations entering the garnet X-site, together with non-linear weighted least-squares fits to Eqn. 2.1. Error bars (shown if bigger than symbols) are 1s .

Figure 2.5. (d - e) Onuma diagrams for experiments 13 and 14 showing partition coefficients for trivalent cations entering the garnet X-site, together with non-linear weighted least-squares fits to Eqn. 2.1. Error bars (shown if bigger than symbols) are 1s .

As illustrated in Figure 2.6a, fitted values of r0 vary systematically with garnet composition. Linear regression of r0 against garnet composition gives

r0 = 0.993 - 0.0628XPy Å (2.2)

Figure 2.6a also shows variations in crystallographic measurements of the size of the garnet X-site with major element composition. Garnet X-sites are not spherical; there are two non-equivalent sets of four bond distances around the divalent cation leading to a range in X-site radii, shown as the grey area in Figure 2.6a. X-site radii for pure pyrope and pure grossular, predicted from the partitioning data using Eqn. 2.2 (0.930 Å and 0.993 Å respectively), are well within the range of radii derived from crystallographic measurements. We conclude that values of r0 determined from fits to the trace element data are a good approximation of the true variation in the effective radius of the garnet X-site. Although beyond the scope of this paper, this direct relationship probably extends to natural situations (i.e., garnets containing significant amounts of Fe, Mn and/or Cr), as is the case for clinopyroxene (see Wood and Blundy 1997).

Figure 2.6b displays the variation of D0 with garnet composition. D0 is influenced by small variations in temperature as well as crystal and melt composition. Van Westrenen et al. (1997) showed that D0 generally increases with decreasing temperature, partly due to the high enthalpies of fusion of end member garnets. In this study, however, the pyrope-rich garnets, synthesised at 1560-1565 oC, have a higher D0 than the more grossular-rich garnets formed at temperatures of 1530-1545 oC. This is a reflection of the importance of configurational entropy effects in both crystal and melt (Blundy et al. 1996).

Figure 2.6. (a) Variations of r0 along the pyrope-grossular join. Error bars are 1s . Solid line is a linear fit to r0 data from Table 2.6. Shaded area shows expected variation in X-site radius in pyrope-grossular solid solutions, taking into account the variations of cation-oxygen distances around the end-member X-sites taken from Smyth and Bish (1988), and using r_oxygen = 1.38 Å. (b) Variation of D0 along pyrope-grossular join. Error bars are 1s . T in ^oC is shown adjacent to each point.

Configurational effects are anticipated in this study, because of the very large compositional range of our garnet crystals and melts. Specifically, the higher D0 values for Py82 and Py84 are a consequence of the fact that the melts in these experiments are not on the pyrope-grossular join, as opposed to the melts in the other experiments. Quantification of these effects requires application of activity-composition relations for both garnet and melt. This is discussed in Chapter 6.

Finally, let us consider our derived values of Young’s modulus E. Blundy and Wood (1994) and Wood and Blundy (1997) showed that derived E values for plagioclase/melt and clinopyroxene/melt partitioning of 1+, 2+ and 3+ cations can be rationalised using the relationships established by Anderson and Anderson (1970) and extended by Hazen and Finger (1979). Anderson and Anderson (1970) showed that the bulk moduli K of many different oxides depend linearly on cation charge (Zc) and are inversely proportional to molecular volume V0:

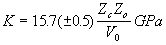(2.3)

where Zo is the charge on the oxygen anion. Hazen and Finger (1979) extended this work to cations co-ordinated by oxygen in silicates and oxides and, using the fact that V0 is approximately equal to the interatomic (cation-oxygen) distance cubed (d3), they obtained

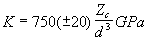(2.4)

with d in Å. By using the identities E = 3K(1 - 2s ) (with s , Poisson’s ratio, taken as 0.25) and r0 + roxygen = d (with roxygen = 1.38 Å after Shannon 1976), best-fit values for E and r0 can be compared with mineral physics data represented by Eqn. 2.4. Figure 2.7 is a plot of bulk modulus K versus Zc / d3, and shows the curve defined by Eqn. 2.4 together with data from Blundy and Wood (1994) and Wood and Blundy (1997), and our garnet-melt data from Table 2.6. It is clear from Figure 2.7 that our new data extend the range seen for clinopyroxene-melt partitioning to higher values of K. It is also apparent that a large positive deviation from the Hazen and Finger relation occurs at higher values of Zc / d3. Furthermore, the X-sites in both our pyrope-rich (Py₈₄ and Py₈₂) and grossular-rich (Py₉) garnets appear stiffer than our intermediate (Py₆₅ and Py₆₀) garnets.

With respect to the high values of K for pyrope-rich garnets, it is well documented that pyrope does not follow the Hazen and Finger relation (e.g. Leger et al. 1990; Olijnyk et al. 1991). The published data, however, show pyropic garnets to be less compressible than grossular, and this is not the case in our experiments (Fig. 2.7). The high values of K derived for pyrope-rich garnets from this study are not unique - fitting of Eqn. 2.1 to other well-constrained experimental garnet-melt partitioning data with similar high values of Z_c/d³ (Hauri et al. 1994; Withers 1997) gives K values in the range of 390-450 GPa. Furthermore, preliminary static lattice energy simulations (Van Westrenen et al. 1998) of the incorporation of trivalent defects into pyrope X-sites, show the same high values for K. At present we have no satisfactory explanation for this phenomenon, although the heterovalent nature of the substitution, and consequent requirement for charge balance through coupled substitution, is probably an important factor.

Figure 2.7. Site bulk modulus K derived from partitioning experiments versus cation charge (Zc) over metal-oxygen distance cubed (d3) for univalent, divalent and trivalent cations in plagioclase and the clinopyroxene M2 site (Blundy and Wood 1994; Wood and Blundy 1997), and trivalent cations in garnet (this study - error bars are 1s ). Note the divergence at higher Zc / d3 values from the linear relationship derived by Hazen and Finger (1979) for cation polyhedra in oxides. Crosses show bulk moduli of end-member minerals albite (Ab), anorthite (An), diopside (D), grossular (G) and pyrope (P). Adapted from Wood and Blundy (1997).

On the other hand, our observations on the non-linearity of K along the pyrope-grossular join are particularly relevant in light of the IR powder absorption spectroscopic study on garnets along the same join by Boffa Ballaran et al. (1999). Their data show a pronounced softening of low-frequency IR modes in intermediate pyrope-grossular garnets. According to Boffa Ballaran et al. (1999), this mode softening could be a result of an incipient phase transition in intermediate pyrope-grossular garnets caused by local structural heterogeneities. Carpenter and Salje (1998) point out that close to phase transition points elastic constants can go to zero, or at least become very small. This ‘softening’ of structures close to phase transition points is consistent with the lower values of E observed for intermediate pyrope-grossular garnets in our experiments (Fig. 2.7), and reinforces our proposal that trace element partitioning experiments can provide structural information relevant to mineral physics.

With respect to a garnet-melt partitioning model, it is therefore not viable to constrain E in Eqn. 2.1 by the Hazen and Finger relationship (Eqn. 2.4). Work needs to focus on finding a more general relationship between K, Zc and d that is valid for garnet and other relatively incompressible phases (i.e., at relatively high values of Zc / d3). It should then be possible to put tighter constraints on E for univalent and divalent cations. Without these constraints, fitting Eqn. 2.1 to partitioning data for these cations is difficult because of the small number of elements present in our experiments. Partition coefficients for 4+ cations (Zr, Hf, Ti, U, and Th) do not show the regular pattern in D - r space observed for the trivalent cations. This is mainly caused by the fact that these elements enter sites other than the X-site (e.g. Ti⁴⁺ goes mainly into the Z-site), so that observed D’s are a sum of D’s on the two sites. We have, therefore, made no attempt to fit 4+ D’s to Eqn. 2.1.

Although our experiments were done in a simple system and exhibit a wide compositional range, we argue that our results have important implications for garnet/melt partitioning in natural systems. In mantle garnets (i.e., garnets from garnet peridotites and group-A eclogites), generally over 60-90% of the X-site is occupied by Mg and Ca, the other 10-40% taken up by Fe2+ and Mn2+ (e.g., Mottana 1986). The compositional variation of mantle garnets, combined with the significant effects of composition on partitioning seen in this study call into question any mantle melting model using fixed and constant garnet-melt partition coefficients.

Garnet-melt trace element partition coefficients, obtained from isobaric (3 GPa), near-isothermal (1545 ± 15 ºC) experiments in the simple system CMAS, show significant variations as a function of garnet Mg / (Mg + Ca) content. Using the mineral-melt partitioning model of Blundy and Wood (1994), a quantitative expression was derived linking the optimum radius r₀ to garnet Py and Gr content for trivalent cations substituting in the garnet X-site (REE, Sc, In, Y). Garnets with intermediate compositions (Py₆₀Gr₄₀ and Py₆₅Gr₃₅) show anomalously low values of the apparent X-site Young’s modulus, which may be related to the proximity of a phase transition in these garnets.