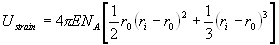Van Westrenen, W., Allan, N.L., Blundy, J.D., Purton, J.A. and Wood, B.J. (2000b) Atomistic simulation of trace element incorporation into garnets - comparison with experimental garnet-melt partitioning data. Geochim. Cosmochim. Acta 64, 1629-1639. Copyright © Elsevier Science Ltd.

4.1 Abstract

We have studied the energetics of trace element incorporation into pure almandine (Alm), grossular (Gros), pyrope (Py) and spessartine (Spes) garnets, by means of computer simulations of perfect and defective lattices in the static limit. The simulations use a consistent set of interatomic potentials to describe the non-Coulombic interactions between the ions, and take explicit account of lattice relaxation associated with trace element incorporation. The calculated relaxation (strain) energies U_rel are compared to those obtained using the Brice (1975) model of lattice relaxation, and the results compared to experimental garnet-melt trace element partitioning data interpreted using the same model.

Simulated U_rel associated with a wide range of homovalent (Ni, Mg, Co, Fe, Mn, Ca, Eu, Sr, Ba) and charge-compensated heterovalent (Sc, Lu, Yb, Ho, Gd, Eu, Nd, La, Li, Na, K, Rb) substitutions onto the garnet X-sites show a near-parabolic dependence on trace element radius, in agreement with the Brice model. From application of the Brice model we derived apparent X-site Young’s moduli E_X(1+, 2+, 3+) and the ‘ideal’ ionic radii r₀(1+, 2+, 3+), corresponding to the minima in plots of U_rel vs. radius. For both homovalent and heterovalent substitutions r₀ increases in the order Py - Alm - Spes - Gros, consistent with crystallographic data on the size of garnet X-sites and with the results of garnet-melt partitioning studies. Each end-member also shows a marked increase in both the apparent E_X and r₀ with increasing trace element charge (Z_c). The increase in E_X is consistent with values obtained by fitting to the Brice model of experimental garnet-melt partitioning data. However, the increase in r₀ with increasing Z_c is contrary to experimental observation.

To estimate the influence of melt on the energetics of trace element incorporation, solution energies (U_sol) were calculated for appropriate exchange reactions between garnet and melt, using binary and other oxides to simulate cation co-ordination environment in the melt. U_sol also shows a parabolic dependence on trace element radius, with inter-garnet trends in E_X and r₀ similar to those found for relaxation energies. However, r₀(i+) obtained from minima in plots of U_sol vs. radius are located at markedly different positions, especially for heterovalent substitutions (i = 1, 3). For each end-member garnet, r₀ now decreases with increasing Z_c, consistent with experiment. Furthermore, although different assumptions for trace element environment in the melt, e.g. REE³⁺ (VI) vs. REE³⁺ (VIII), lead to parabolae with differing curvatures and minima, relative differences between end-members are always preserved.

We conclude that: (1) The simulated variation in r₀ and E_X between garnets is largely governed by the solid phase. This stresses the overriding influence of crystal local environment on trace element partitioning. (2) Simulations suggest r₀ in garnets varies with trace element charge, as experimentally observed. (3) Absolute values of r₀ and E_X can be influenced by the presence and structure of a coexisting melt. Thus, quantitative relations between r₀, E and crystal chemistry should be derived from well-constrained systematic mineral-melt partitioning studies, and cannot be predicted from crystal-structural data alone.

How trace elements partition between minerals and silicate melts is of considerable current interest. For example, garnet-melt and clinopyroxene-melt partition coefficients (D’s) play a critical role in the ongoing debate about the postulated involvement of garnet in the formation of mid-ocean ridge basalt (MORB). Specifically, U-Th disequilibria in present-day MORB (Bourdon et al. 1996) require a mineral phase in the MORB source that retains U preferentially over Th, and, until recently, experimental evidence (e.g. Beattie 1993; LaTourrette et al. 1993) suggested that only garnet meets this requirement. Similarly, Sm-Nd and Lu-Hf systematics (e.g. Salters 1996) and MORB REE patterns (Shen and Forsyth 1995) have been explained by the presence of garnet in the MORB source, and several percent melting in the garnet peridotite stability field has been incorporated in several MORB melting models (e.g. McKenzie and O’Nions 1991; Shen and Forsyth 1995). However, Robinson and Wood (1998) show that melting anhydrous garnet peridotite requires unrealistically high mantle potential temperatures, and Blundy et al. (1998) and Wood et al. (1999) conclude from partitioning experiments that clinopyroxene in the spinel stability field can impose a garnet-like signature on coexisting melts, possibly obviating the need for any garnet in the MORB source. Alternatively, Hirschmann and Stolper (1996), Blichert-Toft et al. (1999) and others address the possible role of garnet pyroxenite veins (comprising up to 5% of the upper mantle) in causing the garnet signature.

A proper evaluation of the roles of garnet and pyroxene require detailed knowledge of the physicochemical principles governing the distribution of trace elements in mineral-melt systems. Considerable progress has been made in recent years (e.g. Wood and Blundy 1997). First, significant improvements in analytical techniques have facilitated accurate experimentation involving large suites of trace elements (e.g. Hart and Dunn 1993). Secondly, the development of a predictive crystal-melt partitioning model by Blundy and Wood (1994) provides a convenient framework for the interpretation of partitioning data. Thirdly, increases in both computer speed and program methodology have made computer simulations of the incorporation of trace elements in crystal structures a feasible option, providing an independent insight into the energetics accompanying substitution in silicates (e.g. Purton et al. 1996; 1997a; 1997b). In this paper, we report computer simulations on trace element incorporation in garnet end-members almandine (Alm, Fe₃Al₂Si₃O₁₂) grossular (Gros, Ca₃Al₂Si₃O₁₂), pyrope (Py, Mg₃Al₂Si₃O₁₂) and spessartine (Spes, Mn₃Al₂Si₃O₁₂). We compare results from our simulations with recent experimental observations, in order to obtain a detailed understanding at the atomistic level of the controlling factors in garnet-melt partitioning.

The model of Blundy and Wood (1994) proposes that crystal chemistry dominates the partitioning behaviour in mineral-melt systems. Wood and Blundy (1997) successfully applied the model to predict clinopyroxene-melt D’s as a function of pressure (P), temperature (T) and bulk composition (X), and we are currently finalising an analogous parameterisation for garnet (Van Westrenen et al. 1999b). The model is based on the observation of Onuma et al. (1968) that mineral-melt D’s for series of isovalent trace elements show a near-parabolic dependence on trace element radius, and invokes the lattice strain model of Brice (1975) to quantify this near-parabolic dependence. Brice (1975) relates the lattice strain energy U_strain, associated with the insertion of a trace element with radius r_i into a spherical site with radius r₀, to the elasticity of the site (Young’s modulus, E) and the size misfit (r_i - r₀) between substituent and host cations:

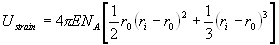(4.1)

where N_A is Avogadro’s constant. The larger the size misfit, or the higher E, the higher the strain energy associated with a substitution, and the lower the affinity of the host structure for a particular trace element. Assuming crystals are far more rigid than melts, the energy associated with the exchange reaction between melt and crystal is dominated by the strain energy U_strain in the crystal. The Blundy and Wood (1994) model thus predicts that the trace element which produces the highest strain energy upon incorporation in a mineral will be the most incompatible, and therefore have the lowest mineral-melt partition coefficient.

Van Westrenen et al. (1999a) have applied the Blundy and Wood (1994) model to a series of near-isothermal, isobaric garnet-melt partitioning experiments along the pyrope-grossular join, involving a wide range of homovalent and heterovalent substitutions into the garnet X-site. Values of r₀ derived for trivalent trace elements show a systematic dependence on garnet composition, consistent with the observation that the X-site radius increases from pyrope (~ 0.89 Å) to grossular (~1.03 Å). Figure 4.1 shows data from one of the experiments, together with curves fitted using the Blundy and Wood (1994) model. The near-parabolic dependence of U_strain on r_i predicted by Eqn. 4.1 is clearly visible for divalent and trivalent trace elements. The apparent site modulus E_X increases with increasing trace element charge, as observed for other minerals (e.g. Wood and Blundy 1997). Interestingly, fitted values of r₀ show a significant variation with trace element charge, with r₀(3+) = 0.935 ± 0.001 Å, r₀(2+) = 0.99 ± 0.03 Å, and r₀(1+) ~ 1.2 Å (based on differences between D_Li and D_K), a feature not observed in clinopyroxene-silicate melt partitioning (Wood and Blundy 1997), but recently documented in wollastonite-carbonate melt partitioning (Law et al. 1999). It is crucial that any predictive garnet-melt partitioning model can rationalise these observations (Van Westrenen et al. 1999b), and the primary aim of the simulations reported here is to suggest explanations for the trends observed in garnet-melt experiments.

Figure 4.1. Experimental garnet-melt partition coefficients D^{Grt / Melt} for 1+, 2+ and 3+ trace elements entering the garnet X-site (data from Van Westrenen et al. 1999a). 1s errors are smaller than symbol size. Curves are weighted least-squares fits to data of the Blundy and Wood (1994) model. Note parabolic dependence of D^{Grt / Melt} on trace element radius.

For the simulations a Born (ionic) model was used, assigning integral ionic charges, based on the accepted chemical valence rules, to all species. To describe non-Coulombic interactions between adjacent ions we used the consistent set of potentials listed in Table 4.1 for all the compounds studied. Cation-oxygen interactions were described by 2-body Buckingham potentials. Account of the oxide ion polarisability was taken using the shell model of Dick and Overhauser (1958), and a three-body O-Si-O bond bending term incorporated. Purton et al. (1996; 1997a) have shown the applicability of these potentials for simulations of oxides (CaO and MgO) and silicates (olivine, orthopyroxene, clinopyroxene). We used the General Utility Lattice Program (GULP; Gale 1997) for all simulations, and Appendix 2 provides sample GULP input files.

Static simulations of perfect lattices give the lattice energy and crystal structure of the low-temperature garnets. In the static limit, the lattice structure is determined by the condition dU / dX_i=0, where U is the internal energy, and the variables {X_i} define the structure (i.e., the lattice vectors, the atomic positions in the garnet unit cell, and the oxygen shell displacements).

Simulated structures for Py, Alm, Spes and Gros were used as a basis for defect energy calculations. In every computational run, one or more defects are introduced into the crystal, e.g., for homovalent substitution, one divalent cation at the X-site of a perfect garnet lattice was replaced by one trace element divalent cation. Initial, unrelaxed defect energies U_def(i) were calculated without allowing any atoms to move. The total energy of the defective system was then minimised by allowing the surrounding ions to relax to accommodate the misfit cation(s). Positions of cores and shells of atoms around the introduced defect(s) were optimised using the two-region approach (Catlow and Mackrodt 1982). In the inner region, containing the defect(s) and typically totalling 320-380 ions, the lattice relaxation is largest and the elastic force equations are solved explicitly (i.e. the force on all ions in this region is required to be zero). In the outer region, comprising 1200-1700 ions, lattice relaxation was assumed to be much smaller, and estimated using the Mott-Littleton approximation (Mott and Littleton 1938). The number of ions is sufficient to ensure convergence of defect energies with region size. After convergence, final, relaxed defect energies U_def(f) were obtained.

For heterovalent substituents, to ensure overall charge balance, a second trace element was inserted simultaneously into the crystal, as near as possible to the first defect. Previous work (Purton et al. 1997a) has demonstrated the importance of defect association in forsterite and diopside, and so we present results here only for associated defects. For trivalent trace cations, a Na or Li cation was placed on an adjacent X-site, or an Al cation on an adjacent Z-site (YAG-type substitution). For univalent trace cations, compensation was achieved by a trivalent cation on the X-site or an Si replacing Al on the Y-site (majorite-type substitution). This choice of compensating defect is consistent with the results of Purton et al. (1997a), who evaluated the energetics of a wide range of possible substitutions in forsterite and diopside. For trivalent trace cations, the favoured mechanism is charge-balancing with a Li on the X-site in all end-member garnets. For univalent cations, the most energy-effective charge-balancing mechanism involves a trivalent cation on the X-site, but the trivalent cation differs from end-member to end-member (Lu for Py, Yb for Alm and La for Spes and Gros). In pyrope, but not the other garnets, majorite-type substitution is comparable in energy.

Although all the simulations reported in this paper are in the static limit, defect energies in this limit have been shown to be a good approximation to defect enthalpies at elevated temperatures (Taylor et al. 1997). For more details on defect energy calculations in silicates the reader is referred to Patel et al. (1991) and Purton et al. (1996; 1997a).

Table 4.2 shows calculated lattice parameters for all end-member garnets, which are reproduced to within 1.6 % of the experimental values. Simulated bulk moduli K are 8-20% larger than those measured at room pressures and temperatures, but the differences are largely due to: (1) The difference in temperature between the simulations, which relate to the static limit (i.e. T = 0 in the absence of lattice vibrations), and experiment. Garnet bulk moduli increase by up to 7 GPa per 300 K decrease in temperature (e.g. Anderson and Isaak 1995). (2) Small differences between measured and simulated lattice parameters.

Table 4.3 lists initial (unrelaxed) and final (relaxed) defect energies (U_def(i) and U_def(f)) for all substitutions in the four end-member garnets considered in this study. First, for a given valence, there is a linear increase in U_def(f) with increasing ionic radius (Purton et al. 1996; 1997a). Secondly, for heterovalent substitutions the magnitude of the defect energies depends on the charge-balancing mechanism. Also tabulated in Table 4.3 is the relaxation energy U_rel, which is the energy released by the garnet lattice as the ions surrounding the defect(s) move to accommodate the misfit. U_rel, equivalent to U_strain in

Eqn. 4.1, is defined as U_def(i) - U_def(f), and is always positive. As expected, U_rel is also dependent on the charge-balancing mechanism; in what follows we shall only discuss data pertaining to the charge-balancing mechanisms which give the lowest defect and relaxation energies. Fig. 4.2 shows the variation of U_rel for univalent, divalent and trivalent trace elements with trace cation (eight-fold coordinated) radius r_i (Shannon 1976) for the four garnets. The general characteristics of these plots are similar for each end-member: for each series of trace elements with the same charge, U_rel shows a near-parabolic dependence on r_i. It is important to stress that the simulations do not involve the use of any concept of ionic radius. As such, Fig. 4.2 provides independent evidence for the applicability of the form of the Brice (1975) model (Eqn. 4.1) to relaxation energies in defective garnet lattices.

We fitted the Brice model (Eqn. 4.1) to each series of relaxation energies. Fitted values for apparent X-site Young’s modulus E_X and ‘ideal’ ionic radius r₀ are given in Table 4.4, and shown by the curves in Fig. 4.2.

Differences in crystal-chemistry between the four garnets are reflected in trends of the fitted r₀ and E_X. For isovalent substituents (circles in Fig. 4.2) the position of the minimum increases from pyrope (r₀ » r_Mg) to grossular (r₀ » r_Ca). This trend in r₀ is compatible with crystallographic data on garnet X-site radii (e.g. Smyth and Bish 1988) and with the variation in cell parameters for simulated garnets (Table 4.2). The variation in apparent E_X mirrors that of the calculated bulk moduli of the four garnets, which decrease from pyrope to grossular. The experimental bulk modulus of grossular is evidently lower that that of pyrope, however the range in values reported for the four compounds (Table 4.2) is such that further comparison with our calculations is not possible. Simulated pyrope

Figure 4.2. Simulated relaxation energies (symbols) for 1+, 2+ and 3+ trace elements in (a) Pyrope, (b) Almandine, (c) Spessartine, (d) Grossular. Data are from Table 4.3. Curves are least-squares fits (Table 4.4) to data of the Brice (1975) model, Eqn. 4.1.

garnet is the least compressible, which leads to a more marked discrimination between misfit cations at the pyrope X-site, and thus the highest E_X in Table 4.4.

For the heterovalent substitutions r₀ increases in the order Py < Alm < Spes < Gros, as also observed for isovalent substitution, while the apparent E_X decreases. As mentioned earlier, all heterovalent results are for the associated pair of defects involving the heterovalent substituent and the charge-compensating defect (Li⁺ for 3+ substituents and REE³⁺ for 1+ substituents). For a given garnet, the apparent E_X increases with increasing charge in each garnet (e.g. for Spes, E_X ranges from 159 ± 78 GPa for univalent defects to 651 ± 12 GPa for trivalent defects), entirely consistent with experimental observations: The apparent E_X(3+) derived from 33 published garnet-melt partitioning experiments ranges from 419 ± 65 to 870 ± 174 GPa, while values for E_X(2+) are in the range 125 ± 14 to 334 ± 12 GPa. r₀ increases systematically with defect ionic charge, with r₀(2+) always equal to the radius of the host cation, as found for other minerals and oxides (Purton et al. 1996; 1997a).

The increase in r₀ with increasing trace element charge is opposite to the trend observed in garnet-melt partitioning data (Van Westrenen et al. 1998 and Fig. 4.1). To investigate this discrepancy further, we performed two additional series of defect calculations on spessartine, assigning charges of 1+ and 3+ respectively to the divalent trace elements, without varying the short-range interatomic potentials listed in Table 4.1. No charge-balancing substitutions were made. Resulting defect and relaxation energies are given in Table 4.5. Figure 4.3 shows a plot of U_rel versus trace element radius r. For clarity, we assigned the same radii to 1+ and 3+ cations as to the corresponding 2+ cation. Again, r₀(1+) < r₀(2+) < r₀(3+). Since the non-Coulombic interactions are the same for

Figure 4.3. Influence of charge on relaxation energies for trace elements in spessartine (symbols). Data are from Table 4.5. Curves are least-squares fits to data using Eqn. 4.1. Note increase in r₀ (and E_X) with charge.

each series of defects, the variations in r₀ with charge in Fig. 4.3 must be caused solely by the variation in trace element charge. These charged defects impose an extra strain on the structure, since after relaxation the positions of the oxygens nearest the defect have changed from those adopted when divalent cations occupy the X-site.

The result of increasing the charge of the substituent cation is to create a positively charged defect, which exerts an additional Coulombic attraction on these neighbouring oxygen anions, in this case on the 8 oxygens around the dodecahedral spessartine X-site. Decreasing the charge of the substituent ion creates a negatively charged defect, which has the opposite effect on the neighbouring oxygens. Consequently, the structure can more readily accommodate larger 3+ cations (positively charged defects) and smaller 1+ cations (negatively charged defects), leading to the observed increase in r₀ with trace element charge seen in Figs. 4.2 and 4.3.

It is thus possible to explain the variation in r₀ with trace element charge seen in the calculated relaxation energies plotted in Figs. 4.2a-4.2d. However, the discrepancy between simulation and experiment, which indicates r₀(1+) > r₀(2+) > r₀(3+), remains. A possible reason for this is that, so far, we have looked at energies calculated purely from solid garnet properties, ignoring the presence of an additional phase (i.e. melt) in the experiments. In the next section we address the influence of the melt, via the calculation of solution energies, and provide a possible explanation for the experimental trend in r₀ seen in Fig. 4.1.

Relaxation energies are a function only of the properties of the solid phase. In garnet-melt systems, however, partitioning of trace elements involves (i) removal of the element(s) from the melt, (ii) incorporation of the element(s) into the garnet structure by a substitution mechanism (as modelled in our simulations) and (iii) insertion of the host cation(s) into the melt. To assess the possible influence of melt presence on our results, we have calculated trace element solution energies (U_sol), making a series of assumptions as to the environment of the trace elements in the melt. These calculations are a closer approximation to the complete cation exchange process (Purton et al. 1996).

For homovalent substitutions, processes (i) to (iii) can be described by the substitution reaction (in this case for defect J²⁺ replacing Mg²⁺ in pyrope)

JO(m) + Mg₃Al₂Si₃O₁₂(s) = JMg₂Al₂Si₃O₁₂(s) + MgO(m), (4.2)

We approximate U_sol (i.e. the energy associated with reaction 4.2) by

U_sol = U_def(J) + U_lat(MgO) – U_lat(JO) (4.3)

As a first approximation, then, we have assumed that the local environments of Mg and J in a melt are equivalent to their environments in the corresponding (solid) simple oxides MgO and JO. Thus, in addition to the defect energies tabulated in Table 4.3, differences between the lattice energies U_lat of the host and trace element oxides contribute to U_sol. Explicit inclusion of the heats of fusion of these oxides (Aylward and Findlay 1994) makes little difference. For example, considering molten rather than solid JO and MgO in Eqn. 4.2, the solution energy for Sr at garnet X-sites changes by only about 10 kJ mol^-1.

The corresponding reactions for trivalent (J³⁺) substitutions are

1/2 Li₂O(m) + 1/2 J₂O₃(m) + Mg₃Al₂Si₃O₁₂(s)

= 2 MgO(m) + (JLiMg)Al₂Si₃O₁₂(s) (4.4)

1/2 Na₂O(m) + 1/2 J₂O₃(m) + Mg₃Al₂Si₃O₁₂(s) =

2 MgO(m) + (JNaMg)Al₂Si₃O₁₂(s) (4.5)

1/2 J₂O₃(m) + 1/2 Al₂O₃(m) + Mg₃Al₂Si₃O₁₂(s) = MgO(m) + SiO₂(m) + (JMg₂)Al₂(Si₂Al)O₁₂(s) (4.6)

for charge-compensation by Li and Na on the X-site, and Al on the Z-site respectively. Corresponding solution energies in this case are approximated by

U_sol = U_def(J+Li) + 2 U_lat(MgO) - 1/2 U_lat(J₂O₃) - 1/2 U_lat(Li₂O) (4.7)

U_sol = U_def(J+Na) + 2 U_lat(MgO) - 1/2 U_lat(J₂O₃) - 1/2 U_lat(Na₂O) (4.8)

U_sol = U_def(J+Al) + U_lat(MgO) + U_lat(SiO₂) - 1/2 U_lat(J₂O₃) - 1/2 U_lat(Al₂O₃) (4.9)

A similar set of equations can be derived for partitioning of univalent trace elements (analogous to Equations 4.4 and 4.5 with J=REE³⁺). Lattice energies for J₂O₃, J₂O and JO, tabulated in Table 4.1, were determined using the same potentials as used for defect calculations. Calculated values of U_sol, which determine the favoured solution and charge-compensation mechanisms, are given in Table 4.3. For example, for trivalent trace elements exchange reaction (4) involving coupled J³⁺/Li⁺ substitution is lowest in energy, as mentioned in an earlier section.

Figure 4.4. Simulated solution energies (symbols) for 1+, 2+ and 3+ trace elements in (a) Pyrope, (b) Almandine, (c) Spessartine, (d) Grossular. Data are from Table 4.3. Curves are least-squares fits (Table 4.6) to data of the Brice (1975) model, Eqn. 4.1.

Solution energies associated with the lowest-energy substitutions are plotted against trace element radius in Fig. 4.4. Clearly, solution energies, like relaxation energies, show a near-parabolic dependence on radius. This result stresses the overriding importance of crystal local environment for trace element partitioning: even when the influence of an (admittedly oversimplified) melt is included, the parabolic dependence on radius, predicted from crystal properties only (Eqn. 4.1), persists.

Fits of simulated U_sol data to Eqn. 4.1 (curves in Fig. 4.4) are given in Table 4.6. Differences in r₀(1+, 2+, 3+) between the garnets follow trends identical to those discussed above for U_rel, with r₀ smallest for Py and largest for Gros. Apparent E_X, obtained from the curvature of the solution energy vs. r_i plots, are now the same within error for all garnets for each series of trace elements with the same charge. For each garnet, the apparent E_X still follow the order E_X(3+) > E_X(2+) > E_X(1+). In contrast, absolute values of r₀(1+), r₀(2+) and r₀(3+) are markedly different from those derived from relaxation energy data (Table 4.4 and Fig. 4.5). For example, in Gros, Na is the 1+ trace element with the lowest U_sol (Fig. 4.4d), while Li has the lowest U_rel(1+) (Fig. 4.2d). Similarly, the 3+ trace element with the lowest U_sol in Gros is Yb (Fig. 4.4d), whereas La has the lowest U_rel (Fig. 4.2d). The latter observation is in good agreement with experimental garnet-melt partitioning data, which always show a maximum close to Yb, and not La. The size of these shifts is not the same for each mineral group; for example, both U_rel and U_sol for trivalent cations in the Ca sites in diopside (Purton et al. 1997a) and wollastonite (K. Law, pers. comm.) have minima close to La.

Interestingly, in a given end-member garnet variations in fitted r₀ with trace element charge, obtained from fitting U_sol, show a different trend from that seen in U_rel (Fig. 4.3), which we have already discussed. This is illustrated in Fig. 4.5. r₀(3+) is now

Figure 4.5. Fitted values of r₀ as a function of trace element charge. U_rel and U_sol data (circles and triangles) taken from Tables 4.4 and 4.6, experimental garnet-melt partitioning data (open squares) from Van Westrenen et al. (1999a) (Gros: experiment 13, producing Py₉Gros₉₁; Py: experiment 11, producing Py₈₄Gros₁₆). Dashed and solid lines show trends in simulation and experiment, respectively.

within error of or smaller than r₀(2+), which in turn appears smaller than r₀(1+). This is much closer to what is observed in fits to experimental garnet-melt partitioning data (Van Westrenen et al. 1998; Fig. 4.1), as well as in fits to data in other mineral-melt systems (e.g. calcite-melt; Law et al. 2000). Evidently the nature of the ‘other phase’ can influence which cation is most easily accommodated into a crystal lattice. Relaxation (strain) energy alone does not take this effect into account.

The success of the Brice equation (Eqn. 4.1), which deals with crystal strain energy only, in rationalising trends in trace element incorporation appears to be caused by a fortunate, but only partial cancellation of energy terms. For example, if we consider again the exchange reaction 4.2 used to approximate isovalent garnet-melt partitioning:

JO(m) + Mg₃Al₂Si₃O₁₂(s) = JMg₂Al₂Si₃O₁₂(s) + MgO(m),

the exchange process involves replacing Mg-O short-range interactions with J-O short-range interactions in the garnet, while simultaneously replacing J-O short-range interactions with Mg-O short-range interactions in the ‘melt’. Very roughly, these replacement energies may cancel, so that the net (solution) energy associated with reaction 4.2, is close to the energy released by the garnet lattice as it accommodates misfit cation J, i.e. the relaxation energy U_rel. In this fortunate, albeit partial, cancellation of terms lies the success of empirical mineral-melt partitioning models, which consider only U_strain = U_rel. This discussion, however, shows that this cancellation is only partial, as shown by the differences between the relaxation and solution energy curves, and will depend on the similarity of melt and crystal environments of the ions involved.

The exchange reactions studied so far make a particularly simple assumption about the nature of the local melt environment of trace elements. We decided to study the effect different melt environments could have on U_sol(3+) by assuming a YAG-type environment for trivalent trace elements in the melt. Exchange reactions and corresponding energies then become

1/2 Li₂O(m) + 1/3 J₃Al₅O₁₂(m) + Mg₃Al₂Si₃O₁₂(s) =

2 MgO(m) + (JLiMg)Al₂Si₃O₁₂(s) + 5/6 Al₂O₃(m),

U_sol = U_def(J+Li) + 2 U_lat(MgO) + 5/6 U_lat(Al₂O₃)

- 1/3 U_lat(J₃Al₅O₁₂) - 1/2 U_lat(Li₂O) (4.10)

1/2 Na₂O(m) + 1/3 J₃Al₅O₁₂(m) + Mg₃Al₂Si₃O₁₂(s) =

2 MgO(m) + (JNaMg)Al₂Si₃O₁₂(s) + 5/6 Al₂O₃(m),

U_sol = U_def(J+Na) + 2 U_lat(MgO) + 5/6 U_lat(Al₂O₃)

1/3 U_lat(J₃Al₅O₁₂) - 1/2 U_lat(Na₂O) (4.11)

1/3 J₃Al₅O₁₂(m) + 1/2 Al₂O₃(m) + Mg₃Al₂Si₃O₁₂(s) =

MgO(m) + SiO₂(m) + (JMg₂)Al₂(Si₂Al)O₁₂(s) + 5/6 Al₂O₃(m),

U_sol = U_def(J+Al) + U_lat(MgO) + U_lat(SiO₂)

+ 1/3 U_lat(Al₂O₃) - 1/3 U_lat(J₃Al₅O₁₂) (4.12)

The co-ordination number of J³⁺ in our ‘melt component’ (J₃Al₅O₁₂) is now 8, as opposed to 6 in the case of J₂O₃ melt components. This is obviously an extreme case, and we do not propose that trivalent trace elements have a YAG-type local environment in real silicate melts. Nevertheless, it is illustrative to assess the effect on the calculated solution energies. Lattice energies for YAG-type components, again taken from GULP simulations, and calculated solution energies are given in Table 4.7, and shown in Fig. 4.6 for Py and Gros. Fits of Eqn. 4.1 to the data are given in Table 4.6. The parabolic dependence of U_sol on radius is again preserved, and r₀(3+) increases systematically from Py to Gros. However, Fig. 4.6 also shows that r₀(3+) and apparent E_X(3+) are different from those assuming simple oxide melt environments. The most compatible trivalent cation in Gros changes from Yb (Fig. 4.4) to Gd (Fig. 4.6), and values of apparent E_X(3+) (211 - 240 GPa) are unrealistically low compared with experimental data. Although trends in r₀ and apparent E_X are directly related to trends in crystal-chemistry, absolute values of r₀ and apparent E_X therefore depend on the nature and coordination environment of the phase with which the trace element is being exchanged.

We have not so far explicitly discussed the relative magnitudes of the partition coefficients for differently charged ions, since we have concentrated on the variation of D with ion size for a given charge. The experimental variation in D with charge for given size (Fig. 4.1) is not always reproduced in the simulations. For example, all calculated solution energies for 3+ ions indicate that 2+ ions are more soluble in garnet than 3+ cations, but experimentally some small 3+ cations have higher values of D. Experimentally, the values of the maxima in the parabolae in Onuma diagrams are very sensitive to temperature and pressure (Wood and Blundy 1997), and all the calculations reported here are in the static limit and zero pressure. In addition, calculated solution energies reflect small differences between a number of large quantities, which differ with trace element charge since the solution mechanism changes. Calculated variations in solubility with size for a given charge would therefore be expected to be more reliable than those with charge for a given size.

Figure 4.6. Calculated solution energies for trivalent trace elements (J³⁺) in Pyrope and Grossular using two different assumptions about trace element melt environment as discussed in the text: J₂O₃ (open symbols, data from Table 4.3) and J₃Al₅O₁₂ (filled symbols, data from Table 4.7). Curves are least-squares fits (Table 4.6) to data of the Brice (1975) model, Eqn. 4.1.

Both experimental data (Fig. 4.1) and simulated U_sol data (Figs. 4.4, 4.5, 4.6) strongly suggest that r₀ in mineral-melt systems varies considerably with trace element charge. The nature of this variation depends both on crystal structure and on the nature of the melt. The successful application of the Blundy and Wood (1994) model to trace element partitioning between clinopyroxene (Wood and Blundy 1997), garnet (Van Westrenen et al. 1999b) and a wide range of anhydrous silicate melt compositions, suggest that the local environment of trace elements in these melts does not vary significantly. However, our simulations suggest that it is possible that relationships between mineral composition and r₀ and E are not transferable to, for example, systems with hydrous or carbonatitic melts. This implies that quantitative relations between r₀, E and crystal chemistry should be derived from well-constrained systematic mineral-melt partitioning studies, and cannot be predicted from crystal-structural data alone (e.g. Bottazzi et al. 1999; Tiepolo et al. 1998).

In this paper, we have demonstrated the ability of static lattice energy simulations on end-member garnets to reproduce trends in high-temperature, high-pressure garnet-melt partitioning experiments. The following conclusions can be drawn from the integration of simulations and experiments: (1) Variations in r₀ and E_X between different garnet end-members result from variations in crystal-chemistry. This confirms the importance of crystal local environment on trace element partitioning, and allows rationalisation of garnet-melt partitioning data using the Brice (1975) model (Eqn. 4.1). (2) Simulations strongly suggest r₀ in garnets varies with trace element charge, as observed experimentally. (3) Absolute values of r₀ and E_X can be influenced by the presence and structure of a coexisting melt. This precludes the use of crystal-structural data alone to predict r₀. (4) Trace element incorporation in mineral-melt systems is an exchange process and therefore solution energies (which take account of both crystal lattice relaxation and this exchange with the melt) are more relevant to partitioning studies than relaxation energies (which are based on lattice relaxation only). Further work should be directed towards high-temperature simulations that explicitly take account of lattice vibrations and cation ordering in both solid and molten phases (e.g. Purton et al. 2000).